Page 306 - Instrumentation Reference Book 3E

290 Temperature measurement

one of three fates. A portion may be reflected.
Another portion may be transmitted through the
substance. The remainder will be absorbed and
degraded to heat. The sum of the fraction
reflected r, the fraction transmitted t and the
fraction absorbed a will be equal to the total
amount incident on the substance. Furthermore,
the emittance E of a substance is identical to the
absorptance a, and we can write
&=fl=l-t-V (14.42)
For the blackbody the transmittance and reflec-
tance are zero and the emittance is unity. For any
opaque substance the transmittance is zero and
&=l-T (14.43)
An example of this case is oxidized steel in the
visible and near-infrared where the transmittance
is 0, the reflectance is 0.20 and the emittance is
0.80. A good example of a material whose emit-
tance characteristics change radically with wave-
0 12 3 4 5 6 7 8 9 10 length is glass. Figure 14.59 shows the overall
transmission of soda-lime glass. The reflectance
Wavelength pm of the glass is about 0.03 or less through most of
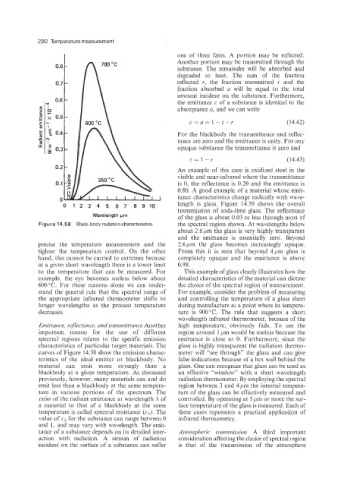
Figure 14.58 Black-body radiation characteristics. the spectral region shown. At wavelengths below
about 2.6 pm the glass is very highly transparent
and the emittance is essentially zero. Beyond
precise the temperature measurement and the 2.6 pm the glass becomes increasingly opaque.
tighter the temperature control. On the other From this it is seen that beyond 4pm glass is
hand, this cannot be carried to extremes because completely opaque and the emittance is above
at a given short wavelength there is a lower limit 0.98.
to the temperature that can be measured. For This example of glass clearly illustrates how the
example, the eye becomes useless below about detailed characteristics of the material can dictate
600°C. For these reasons alone we can under- the choice of the spectral region of measurement.
stand the general rule that the spectral range of For example, consider the problem of measuring
the appropriate infrared thermometer shifts to and controlling the temperature of a glass sheet
longer wavelengths as the process temperature during manufacture at a point where its tempera-
decreases. ture is 900°C. The rule that suggests a short
wavelength infrared thermometer, because of the
En1 it tan ce, reflectance, and tr’ansniit tan ce Another high temperature, obviously fails. To use the
important reason for the use of different region around 1 pm would be useless because the
spectral regions relates to the specific emission emittance is close to 0. Furthermore, since the
characteristics of particular target materials. The glass is highly transparent the radiation thermo-
curves of Figure 14.58 show the emission charac- meter will “see through” the glass and can give
teristics of the ideal emitter or blackbody. No false indications because of a hot wall behind the
material can emit more strongly than a glass. One can recognize that glass can be used as
blackbody at a given temperature. As discussed an effective “window” with a short wavelength
previously, however, many materials can and do radiation thermometer. By employing the spectral
emit less than a blackbody at the same tempera- region between 3 and 4pm the internal tempera-
ture in various portions of the spectrum. The ture of the glass can be effectively measured and
ratio of the radiant emittance at wavelength X of controlled. By operating at 5 pm or more the sur-
a material to that of a blackbody at the same face temperature of the glass is measured. Each of
temperature is called spectral emittance (EX). The these cases represents a practical application of
value of EA for the substance can range between 0 infrared thermometry.
and 1, and may vary with wavelength. The emit-
tance of a substance depends on its detailed inter- Atmospheric transmission A third important
action with radiation. A stream of radiation consideration affecting the choice of spectral region
incident on the surface of a substance can suffer is that of the transmission of the atmosphere