Page 267 - Integrated Wireless Propagation Models

M i c r o c e l l P r e d i c t i o n M o d e l s 245

0 -
-10
-20 -
((} -30 -
"0
ui -40 - �
en
.2 -50 - �
(ij
c �
Ol -60 -
i:i5 �
-70 -
-80 -
�
-90 .
-100 I rb
I I
0 75 1 5 0 225 300 350
r, m
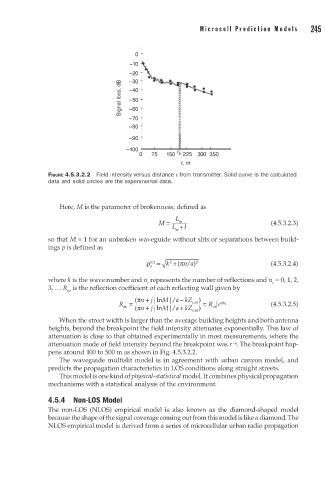
FIGURE 4.5.3.2.2 Field intensity versus distance r from transmitter. Solid curve is the calculated
data and solid circles are the experimental data.

Here, M is the parameter of brokenness, defined as
M = � (4.5.3.2.3)
Lm +l
so that M = 1 for an unbroken waveguide without slits or separations between build­
ings p is defined as

( 4.5.3.2.4)

where k is the wave number and n, represents the number of reflections and n, = 0, 1, 2,
.
3, . . R11, is the reflection coefficient of each reflecting wall given by
R = (rcn + j l lnM I /a - kZ ) = lr.> l e i'fi, (4.5.3.2.5)
EM
n +
a + k
"
' (rc j l lnM I / Z ) f'"'
EM
When the street width is larger than the average building heights and both antenna
heights, beyond the breakpoint the field intensity attenuates exponentially. This law of
attenuation is close to that obtained experimentally in most measurements, where the
q
attenuation mode of field intensity beyond the breakpoint was - . The breakpoint hap­
,
m
pens around 100 to 500 a s shown in Fig. 4.5.3.2.2.
The waveguide multislit model is in agreement with urban canyon model, and
predicts the propagation characteristics in LOS conditions along straight streets.
This model is one kind of physical-statistical model. It combines physical propagation
mechanisms with a statistical analysis of the environment.
4.5.4 Non-LOS Model
The non-LOS (NLOS) empirical model is also known as the diamond-shaped model
because the shape of the signal coverage coming out from this model is like a diamond. The
NLOS empirical model is derived from a series of microcellular urban radio propagation