Page 223 - Introduction to Computational Fluid Dynamics

P1: IWV
CB908/Date
0 521 85326 5
0521853265c06
202
2D CONVECTION – COMPLEX DOMAINS
FUEL MASS FRACTION May 25, 2005 11:10
0.1
0.2

VARIABLE Ψ
0.9 0.3 0.1
0.2
0.5
0.8

0.7 0.6

TEMPERATURE
0.3
0.9 0.1
0.2
0.5

0.8 0.6
0.7

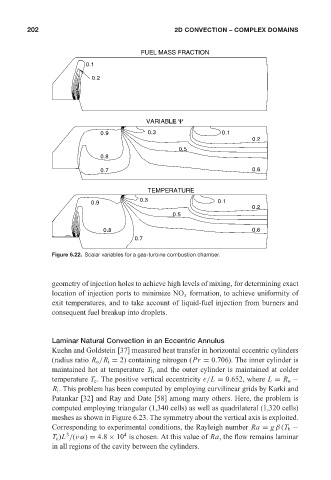
Figure 6.22. Scalar variables for a gas-turbine combustion chamber.

geometry of injection holes to achieve high levels of mixing, for determining exact
location of injection ports to minimize NO x formation, to achieve uniformity of
exit temperatures, and to take account of liquid-fuel injection from burners and
consequent fuel breakup into droplets.

Laminar Natural Convection in an Eccentric Annulus
Kuehn and Goldstein [37] measured heat transfer in horizontal eccentric cylinders
(radius ratio R o /R i = 2) containing nitrogen (Pr = 0.706). The inner cylinder is
maintained hot at temperature T h and the outer cylinder is maintained at colder
temperature T c . The positive vertical eccentricity /L = 0.652, where L = R o −
R i . This problem has been computed by employing curvilinear grids by Karki and
Patankar [32] and Ray and Date [58] among many others. Here, the problem is
computed employing triangular (1,340 cells) as well as quadrilateral (1,320 cells)
meshes as shown in Figure 6.23. The symmetry about the vertical axis is exploited.
Corresponding to experimental conditions, the Rayleigh number Ra = g β (T h −
4
3
T c )L /(να) = 4.8 × 10 is chosen. At this value of Ra, the flow remains laminar
in all regions of the cavity between the cylinders.