Page 227 - Introduction to Computational Fluid Dynamics

P1: IWV
May 25, 2005
11:10
CB908/Date
0521853265c06
206
2.0
2.02.0 0 521 85326 5 2D CONVECTION – COMPLEX DOMAINS
WALL CENTER LINE
WALL
1.61.6 1.6
Mach No
Mach No
1.2 Mach No 1.2
.2
P/P
P / Po P/P o
O
0.88 0.8
0
.
Expt Data
Expt Data
Expt Data
.
0.44 0.4
0

0
.
0.00 0.0
.
0
2
1
7
0
.
.
.
0
0
5
.
0
0.000 0.255 0.500 0.755 1.000 0.00 0.25 0.50 0.75 1.00
0
X/L X / L X/L
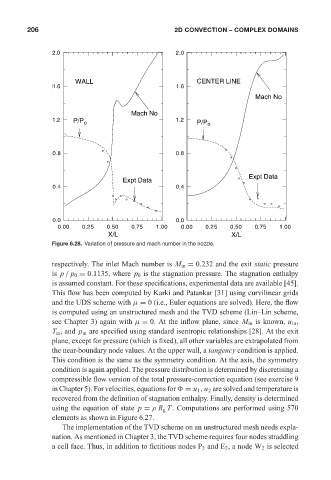
Figure 6.28. Variation of pressure and mach number in the nozzle.
respectively. The inlet Mach number is M in = 0.232 and the exit static pressure
is p / p 0 = 0.1135, where p 0 is the stagnation pressure. The stagnation enthalpy
is assumed constant. For these specifications, experimental data are available [45].
This flow has been computed by Karki and Patankar [31] using curvilinear grids
and the UDS scheme with µ = 0 (i.e., Euler equations are solved). Here, the flow
is computed using an unstructured mesh and the TVD scheme (Lin–Lin scheme,
see Chapter 3) again with µ = 0. At the inflow plane, since M in is known, u in ,
T in , and p in are specified using standard isentropic relationships [28]. At the exit
plane, except for pressure (which is fixed), all other variables are extrapolated from
the near-boundary node values. At the upper wall, a tangency condition is applied.
This condition is the same as the symmetry condition. At the axis, the symmetry
condition is again applied. The pressure distribution is determined by discretising a
compressible flow version of the total pressure-correction equation (see exercise 9
in Chapter 5). For velocities, equations for = u 1 , u 2 are solved and temperature is
recovered from the definition of stagnation enthalpy. Finally, density is determined
using the equation of state p = ρ R g T . Computations are performed using 570
elements as shown in Figure 6.27.
The implementation of the TVD scheme on an unstructured mesh needs expla-
nation. As mentioned in Chapter 3, the TVD scheme requires four nodes straddling
a cell face. Thus, in addition to fictitious nodes P 2 and E 2 , a node W 2 is selected