Page 346 - MATLAB an introduction with applications

Direct Numerical Integration Methods ——— 331

X = X + τ (X − X ) ...(6.54)
t+
t
τ
θ∆t t+ θ ∆ t t

X t+ t∆ X t+θ∆ t
X t

∆
θ
t+ t t+ ∆ t
t τ
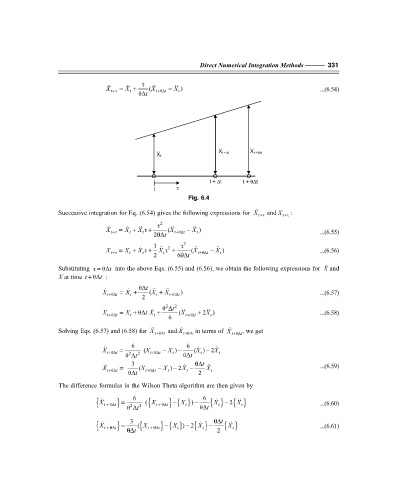
Fig. 6.4
Successive integration for Eq. (6.54) gives the following expressions for X t+ τ and X t+ τ :

X = X + X τ + τ 2 (X − X ) ...(6.55)
t+
t
τ
t
θ
2 ∆t t+ θ ∆ t t

X t+ τ = t X t τ X + 1 X t τ + 2 + τ 3 (X t+ θ ∆ t − X t ) ...(6.56)
2 6θ∆ t

Substituting τ θ = ∆ t into the above Eqs. (6.55) and (6.56), we obtain the following expressions for X and
X at time t + θ∆t :

X = X + θ∆t (X + X ) ...(6.57)
t+
θ∆t
t
2 t t+ θ∆t
2

X = X + θ∆t X + θ∆t 2 (X + 2X ) ...(6.58)
t+
t
θ∆t
t
6 t+ θ∆t t
Solving Eqs. (6.57) and (6.58) for X t+ θ∆t and X t+ θ∆t in terms of X t+ θ∆t , we get

X t+ θ∆t = 6 (X t+ θ∆t − X t ) − 6 (X − t
) 2X
t
2
θ∆t 2 θ∆t

) 2X −
X = 3 (X − X − θ∆ t X ...(6.59)
t+
θ∆t
θ∆t t+ θ∆t t t 2 t
The difference formulas in the Wilson Theta algorithm are then given by

−
−
X
X
{ X t + θ∆t } = 6 ( { X t + θ∆ t } { }) − 6 { } { } ...(6.60)
2 X
t
t
t
2
θ∆t 2 θ∆t
3

−
{ } −
−
{ X t +θ∆ t } = θ∆ t { ( X t +θ∆ t } { }) 2 X t θ∆ t { } ...(6.61)
X
X
t
t
2