Page 190 - MEMS Mechanical Sensors

8.2 Micromachined Accelerometer 179

If the limit x → 0 is taken, (8.3) yields

 V 
x=0
lim
F = F − F  →−2ε A  B V  (8.4)
1
2
 d 2 0 F 
which is a linear, negative feedback relationship.
If we further assume the simplest form of controller, a pure proportional
controller, the feedback voltage can be expressed as V = k x with k as the propor-
F p p
tional gain constant. This can be substituted into (8.2) and (8.4) to plot the resulting
electrostatic force on the proof mass for the exact and linearized solution, respec-
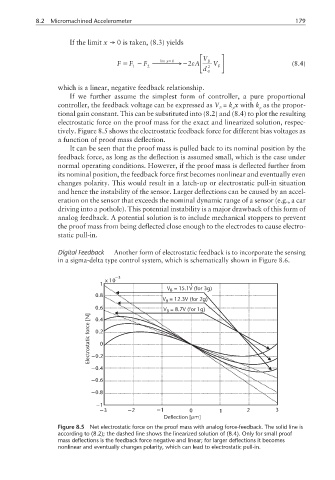
tively. Figure 8.5 shows the electrostatic feedback force for different bias voltages as
a function of proof mass deflection.
It can be seen that the proof mass is pulled back to its nominal position by the
feedback force, as long as the deflection is assumed small, which is the case under
normal operating conditions. However, if the proof mass is deflected further from
its nominal position, the feedback force first becomes nonlinear and eventually even
changes polarity. This would result in a latch-up or electrostatic pull-in situation
and hence the instability of the sensor. Larger deflections can be caused by an accel-
eration on the sensor that exceeds the nominal dynamic range of a sensor (e.g., a car
driving into a pothole). This potential instability is a major drawback of this form of
analog feedback. A potential solution is to include mechanical stoppers to prevent
the proof mass from being deflected close enough to the electrodes to cause electro-
static pull-in.

Digital Feedback Another form of electrostatic feedback is to incorporate the sensing
in a sigma-delta type control system, which is schematically shown in Figure 8.6.

−3
x10
1
V = 15.1V (for 3g)
B
0.8
V = 12.3V (for 2g)
B
0.6 V = 8.7V (for 1g)
B
[N] 0.4
force 0.2
Electrostatic −0.2
0

−0.4
−0.6
−0.8

−1
−3 −2 −1 0 1 2 3
µ
Deflection [ m]
Figure 8.5 Net electrostatic force on the proof mass with analog force-feedback. The solid line is
according to (8.2); the dashed line shows the linearized solution of (8.4). Only for small proof
mass deflections is the feedback force negative and linear; for larger deflections it becomes
nonlinear and eventually changes polarity, which can lead to electrostatic pull-in.