Page 243 - Marks Calculation for Machine Design

P1: Shibu/Sanjay
14:35
January 4, 2005
Brown.cls
Brown˙C05
PRINCIPAL STRESSES AND MOHR’S CIRCLE
225
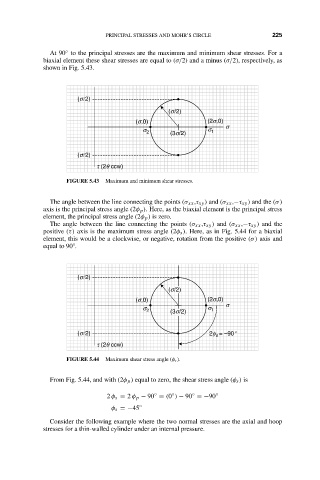
At 90 to the principal stresses are the maximum and minimum shear stresses. For a
◦
biaxial element these shear stresses are equal to (σ/2) and a minus (σ/2), respectively, as
shown in Fig. 5.43.
(s/2)
(s/2)
(s,0) (2s,0)
s
s 2 s 1
(3s/2)
(s/2)
t (2q ccw)
FIGURE 5.43 Maximum and minimum shear stresses.

The angle between the line connecting the points (σ xx ,τ xy ) and (σ xx ,−τ xy ) and the (σ)
axis is the principal stress angle (2φ p ). Here, as the biaxial element is the principal stress
element, the principal stress angle (2φ p ) is zero.
The angle between the line connecting the points (σ xx ,τ xy ) and (σ xx ,−τ xy ) and the
positive (τ) axis is the maximum stress angle (2φ s ). Here, as in Fig. 5.44 for a biaxial
element, this would be a clockwise, or negative, rotation from the positive (σ) axis and
equal to 90 .
◦

(s/2)
(s/2)
(s,0) (2s,0)
s
s 2 (3s/2) s 1

(s/2) 2f = –90∞
s
t (2q ccw)

FIGURE 5.44 Maximum shear stress angle (φ s ).

From Fig. 5.44, and with (2φ p ) equal to zero, the shear stress angle (φ s ) is

◦
◦
◦
2 φ s = 2 φ p − 90 = (0 ) − 90 =−90 ◦
φ s =−45 ◦
Consider the following example where the two normal stresses are the axial and hoop
stresses for a thin-walled cylinder under an internal pressure.