Page 363 - Matrix Analysis & Applied Linear Algebra

5.8 Discrete Fourier Transform 359
Example 5.8.2

Problem: Computing the Inverse Transform. Explain why any algorithm
or program designed to compute the discrete Fourier transform of a vector x
can also be used to compute the inverse transform of x.
Solution: Call such an algorithm FFT (see p. 373 for a specific example). The
fact that
F n x F n x
−1
F n x = =
n n
means that FFT will return the inverse transform of x by executing the following
three steps:
(1) x ←− x (compute x ).
(2) x ←− FFT(x) (compute F n x ).
(3) x ←− (1/n)x (compute n −1 F n x = F −1 x ).
n
T
For example, computing the inverse transform of x =( i 0 −i0 ) is ac-
complished as follows—recall that F 4 was given in Example 5.8.1.
−i 0 0
     
1
 0   −2i  1  2i  −1
x =   , F 4 x =   , F 4 x =   = F 4 x.
i 0 4 4 0
0 −2i 2i
Youmay wish to check that this answer agrees with the result obtained by
directly multiplying F −1 times x, where F −1 is given in Example 5.8.1.
4 4
Example 5.8.3
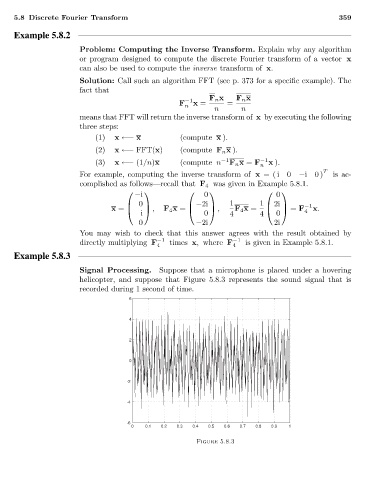
Signal Processing. Suppose that a microphone is placed under a hovering
helicopter, and suppose that Figure 5.8.3 represents the sound signal that is
recorded during 1 second of time.
6

4

2

0

-2

-4

-6
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Figure 5.8.3