Page 366 - Matrix Analysis & Applied Linear Algebra

362 Chapter 5 Norms, Inner Products, and Orthogonality

Therefore, if 0 <f <n, then
F n e i2πft = ne f and F n e −i2πft = ne n−f . (5.8.4)

iθ
iθ
Because cos θ =(e +e −iθ )/2 and sin θ =(e −e −iθ )/2i, it follows from (5.8.4)
that for any scalars α and β,
i2πft −i2πft
e +e nα
F n (α cos 2πft)= αF n = (e f + e n−f )
2 2
and
i2πft −i2πft
e − e nβ
F n (β sin 2πft)= βF n = (e f − e n−f ) ,
2i 2i
so that
2
F n (α cos 2πft)= αe f + αe n−f (5.8.5)
n
and
2
F n (β sin 2πft)= −βie f + βie n−f . (5.8.6)
n
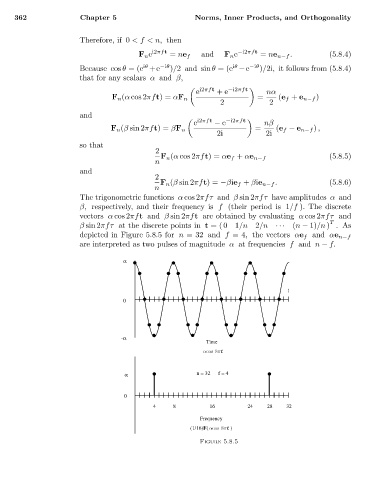
The trigonometric functions α cos 2πfτ and β sin 2πfτ have amplitudes α and
β, respectively, and their frequency is f (their period is 1/f ). The discrete
vectors α cos 2πft and β sin 2πft are obtained by evaluating α cos 2πfτ and
T
β sin 2πfτ at the discrete points in t =( 0 1/n 2/n ··· (n − 1)/n ) . As
depicted in Figure 5.8.5 for n =32 and f =4, the vectors αe f and αe n−f
are interpreted as two pulses of magnitude α at frequencies f and n − f.
α

1
0

-α
Time
αcos πt

α n = 32 f = 4

0
4 8 16 24 28 32
Frequency
(1/16)F(αcos πt )
Figure 5.8.5