Page 367 - Matrix Analysis & Applied Linear Algebra

5.8 Discrete Fourier Transform 363

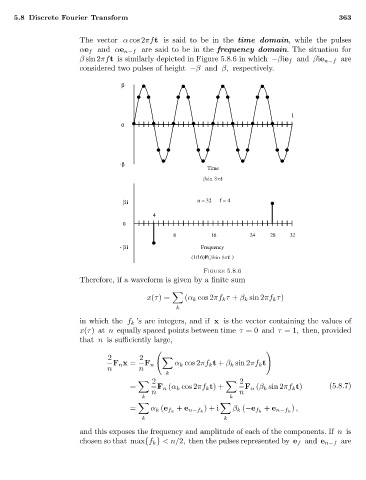
The vector α cos 2πft is said to be in the time domain, while the pulses
αe f and αe n−f are said to be in the frequency domain. The situation for
β sin 2πft is similarly depicted in Figure 5.8.6 in which −βie f and βie n−f are
considered two pulses of height −β and β, respectively.
β

1
0

-β
Time
β sin πt

βi n = 32 f = 4
4
0
8 16 24 28 32
- βi Frequency
β
(1/16)F( sin πt )
Figure 5.8.6
Therefore, if a waveform is given by a finite sum

x(τ)= (α k cos 2πf k τ + β k sin 2πf k τ)
k
in which the f k ’s are integers, and if x is the vector containing the values of
x(τ)at n equally spaced points between time τ =0 and τ =1, then, provided
that n is sufficiently large,

2 2
F n x = F n α k cos 2πf k t + β k sin 2πf k t
n n
k
2 2

= F n (α k cos 2πf k t)+ F n (β k sin 2πf k t) (5.8.7)
n n
k k

= α k (e f k + e n−f k )+i β k (−e f k + e n−f k ) ,
k k
and this exposes the frequency and amplitude of each of the components. If n is
chosen so that max{f k } <n/2, then the pulses represented by e f and e n−f are