Page 236 - Mechanical design of microresonators _ modeling and applications

0-07-145538-8_CH05_235_08/30/05

Resonant Micromechanical Systems

Resonant Micromechanical Systems 235

1.4
I- II 0.8
rω b
1.1

1 1
c t

c l 0.1
5 5
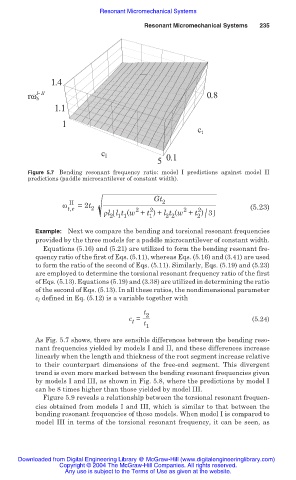
Figure 5.7 Bending resonant frequency ratio: model I predictions against model II
predictions (paddle microcantilever of constant width).

Gt 2
Ȧ II =2t
t,e 2 2 2 2 2 (5.23)
2 /
ȡl l t (w + t ) + l t (w + t ) 3
2 1 1 1 2 2
Example: Next we compare the bending and torsional resonant frequencies
provided by the three models for a paddle microcantilever of constant width.
Equations (5.16) and (5.21) are utilized to form the bending resonant fre-
quency ratio of the first of Eqs. (5.11), whereas Eqs. (5.16) and (3.41) are used
to form the ratio of the second of Eqs. (5.11). Similarly, Eqs. (5.19) and (5.23)
are employed to determine the torsional resonant frequency ratio of the first
of Eqs. (5.13). Equations (5.19) and (3.38) are utilized in determining the ratio
of the second of Eqs. (5.13). In all these ratios, the nondimensional parameter
c l defined in Eq. (5.12) is a variable together with

t 2
c = (5.24)
t t
1
As Fig. 5.7 shows, there are sensible differences between the bending reso-
nant frequencies yielded by models I and II, and these differences increase
linearly when the length and thickness of the root segment increase relative
to their counterpart dimensions of the free-end segment. This divergent
trend is even more marked between the bending resonant frequencies given
by models I and III, as shown in Fig. 5.8, where the predictions by model I
can be 8 times higher than those yielded by model III.
Figure 5.9 reveals a relationship between the torsional resonant frequen-
cies obtained from models I and III, which is similar to that between the
bending resonant frequencies of these models. When model I is compared to
model III in terms of the torsional resonant frequency, it can be seen, as

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.