Page 327 - Mechanical design of microresonators _ modeling and applications

0-07-145538-8_CH06_326_08/30/05

Microcantilever and Microbridge Systems for Mass Detection

326 Chapter Six

1.3
ω b,0 / ω b
1.1
0.01
0.01 c ρ
c E
0.5
0.1
0.1
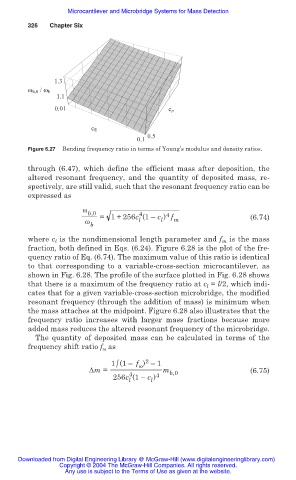
Figure 6.27 Bending frequency ratio in terms of Young’s modulus and density ratios.

through (6.47), which define the efficient mass after deposition, the
altered resonant frequency, and the quantity of deposited mass, re-
spectively, are still valid, such that the resonant frequency ratio can be
expressed as
Ȧ
4
b,0 = 1 + 256c (1– c ) f
4
Ȧ l l m (6.74)
b
where c is the nondimensional length parameter and f is the mass
m
l
fraction, both defined in Eqs. (6.24). Figure 6.28 is the plot of the fre-
quency ratio of Eq. (6.74). The maximum value of this ratio is identical
to that corresponding to a variable-cross-section microcantilever, as
shown in Fig. 6.28. The profile of the surface plotted in Fig. 6.28 shows
that there is a maximum of the frequency ratio at c l = l/2, which indi-
cates that for a given variable-cross-section microbridge, the modified
resonant frequency (through the addition of mass) is minimum when
the mass attaches at the midpoint. Figure 6.28 also illustrates that the
frequency ratio increases with larger mass fractions because more
added mass reduces the altered resonant frequency of the microbridge.
The quantity of deposited mass can be calculated in terms of the
frequency shift ratio f as
Ȧ
2
/
1 (1– f ) –1
Ȧ
ǻm = m b,0 (6.75)
4
256c (1– c ) 4
l
l

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.