Page 84 -

2.5 Designs for Related Problems of an ESEC LD 73
Therefore, the total r and t are given as

r 012 + z 1 r 23 e −i2β 2
r = , (2.38)
1 − r 210 r 23 e −i2β 2
t 012 t 23 e −i2β 2
t = . (2.39)
1 − r 210 r 23 e −i2β 2
where z 1 = t 012 t 210 − r 012 r 210 . (2.40)
Consequently, the total energy reflectivity R and total energy transmission T
are given as
∗
R = rr , (2.41)
N 3 cos θ 3 ∗
T = tt . (2.42)
N 2 cos θ 2
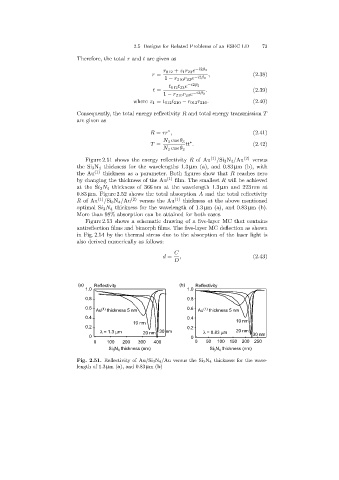
Figure 2.51 shows the energy reflectivity R of Au (1) /Si 3 N 4 /Au (2) versus
the Si 3 N 4 thickness for the wavelengths 1.3 µm (a), and 0.83 µm (b), with
the Au (1) thickness as a parameter. Both figures show that R reaches zero
by changing the thickness of the Au (1) film. The smallest R will be achieved
at the Si 3 N 4 thickness of 366 nm at the wavelength 1.3 µm and 223 nm at
0.83 µm. Figure 2.52 shows the total absorption A and the total reflectivity
R of Au (1) /Si 3 N 4 /Au (2) versus the Au (1) thickness at the above mentioned
optimal Si 3 N 4 thickness for the wavelength of 1.3 µm (a), and 0.83 µm (b).
More than 98% absorption can be attained for both cases.
Figure 2.53 shows a schematic drawing of a five-layer MC that contains
antireflection films and bimorph films. The five-layer MC deflection as shown
in Fig. 2.54 by the thermal stress due to the absorption of the laser light is
also derived numerically as follows:

C
d = , (2.43)
D

(a) Reflectivity (b) Reflectivity
1.0 1.0
0.8 0.8
0.6 Au thickness 5 nm 0.6 Au thickness 5 nm
(1)
(1)
0.4 0.4
10 nm 10 nm
0.2 0.2
l = 1.3 mm 20 nm 30 nm l = 0.83 mm 20 nm
0 0 30 nm
0 100 200 300 400 0 50 100 150 200 250
Si N thickness (nm) Si N thickness (nm)
3 4
3 4
Fig. 2.51. Reflectivity of Au/Si 3N 4/Au versus the Si 3N 4 thickness for the wave-
length of 1.3 µm(a),and 0.83 µm(b)