Page 184 - Modern Control Systems

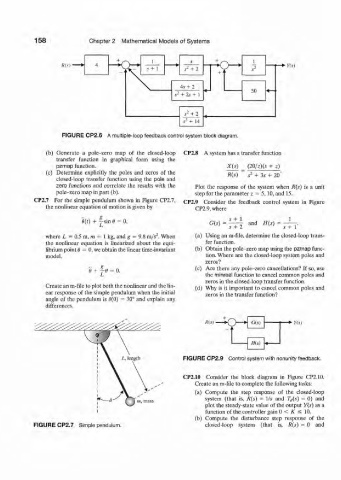
158 Chapter 2 Mathematical Models of Systems

+ r~\ 1 s
Ris) • \r *• ¥(s)
~i\. s+ 1 s 2 + 2 + • s 2

4s+ 2
50
s 2 + 2s + 1

s 2 + 2
,9 3 + 14
FIGURE CP2.6 A multiple-loop feedback control system block diagram.

(b) Generate a pole-zero map of the closed-loop CP2.8 A system has a transfer function
transfer function in graphical form using the
pzmap function. X(s) (20/z)(s + z)
(c) Determine explicitly the poles and zeros of the B{s) ~ s 2 + 3s + 20"
closed-loop transfer function using the pole and
zero functions and correlate the results with the Plot the response of the system when R(s) is a unit
pole-zero map in part (b). step for the parameter z = 5,10, and 15.
CP2.7 For the simple pendulum shown in Figure CP2.7, CP2.9 Consider the feedback control system in Figure
the nonlinear equation of motion is given by CP2.9, where

0(0 + ™ sin 6 0, G(s) = ^ ^ and H(s)
s + 2 s+ 1
where L = 0.5 m, m = 1 kg, and g = 9.8 m/s~. When (a) Using an m-file, determine the closed-loop trans-
the nonlinear equation is linearized about the equi- fer function.
librium point 6 = 0, we obtain the linear time-invariant (b) Obtain the pole-zero map using the pzmap func-
model, tion. Where are the closed-loop system poles and
zeros?
(c) Are there any pole-zero cancellations? If so, use
0 + j6 0.
the minreal function to cancel common poles and
zeros in the closed-loop transfer function.
Create an m-file to plot both the nonlinear and the lin- (d) Why is it important to cancel common poles and
ear response of the simple pendulum when the initial zeros in the transfer function?
angle of the pendulum is 0(0) = 30° and explain any
differences.

lite) • G(s) •*• Y(s)
^ ^ ^ ^ . ^ ^ ^

H(s) 4

FIGURE CP2.9 Control system with nonunity feedback.

CP2.10 Consider the block diagram in Figure CP2.10.
Create an m-file to complete the following tasks:
(a) Compute the step response of the closed-loop
system (that is, R(s) = Vs and 7",,(i) = 0) and
plot the steady-state value of the output Y(s) as a
function of the controller gain 0 < K s 10.
(b) Compute the disturbance step response of the
FIGURE CP2.7 Simple pendulum. closed-loop system (that is, R(s) = 0 and