Page 180 - Modern Control Systems

154 Chapter 2 Mathematical Models of Systems

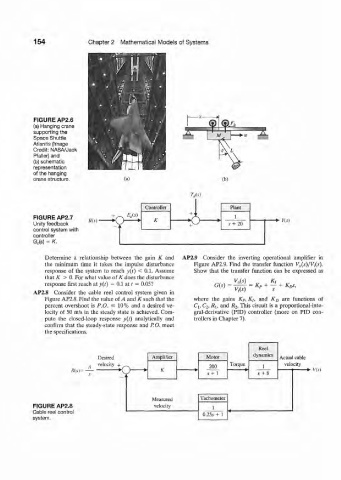
FIGURE AP2.6
(a) Hanging crane
supporting the
Space Shuttle
Atlantis (Image
Credit: NASA/Jack
Pfaller) and
(b) schematic
representation
of the hanging
crane structure. (a) (b)

T d(s)
Controller Plant
, EM +
FIGURE AP2.7 K ( o 1
Unity feedback + s + 20 •+• Y(s)
control system with
controller
G c(s) - K.

Determine a relationship between the gain K and AP2.9 Consider the inverting operational amplifier in
the minimum time it takes the impulse disturbance Figure AP2.9. Find the transfer function VJ,s){Vls),
response of the system to reach y(r) < 0.1. Assume Show that the transfer function can be expressed as
that K > 0. For what value of K does the disturbance
response first reach at y{t) = 0.1 at r = 0.05? G(s) = K, + — + K&,
V,(s)
AP2.8 Consider the cable reel control system given in
Figure AP2.8. Find the value of A and K such that the where the gains K P, K h and K D are functions of
percent overshoot is P.O. £ 10% and a desired ve- Cj, C 2, JRI, and R 2, This circuit is a proportional-inte-
locity of 50 m/s in the steady state is achieved. Com- gral-derivative (PID) controller (more on PID con-
pute the closed-loop response v(f) analytically and trollers in Chapter 7).
confirm that the steady-state response and P. O. meet
the specifications.

Reel
Desired Amplifier Motor dynamics Actual cable
, velocity + 200 Torque 1 velocity
/?(,)= ^ K • > » K • V{s)
-
J * s + 1 j + 8

Measured Tachometer
FIGURE AP2.8 velocity 1
Cable reel control 0.25i + 1
system.