Page 295 - Modern Control Systems
P. 295
Section 4.9 Control System Characteristics Using Control Design Software 2 6 9
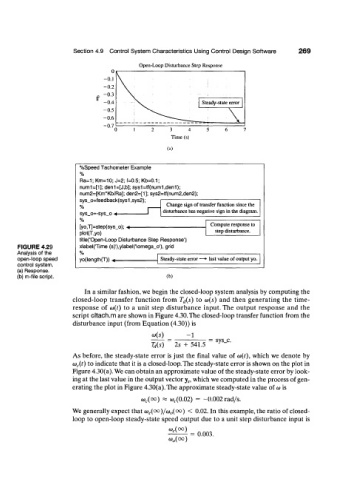
Open-Loop Disturbance Step Response
0
-0.1
-0.2 V j
-0.3
-0.4 \ Steady-state error
-0.5
-0.6 ^ ^ - - _ _ _ \
-0.7
0 1 2 3 4 5 6 7
Time (s)
(a)
%Speed Tachometer Example
%
Ra=1; Km=10; J=2; f=0.5; Kb=0.1;
num1=[1]; den1=[J,b]; sys1=tf(num1,den1);
num2=[Km*Kb/Ra]; den2=[1]; sys2=tf(num2,den2);
sys_o=feedback(sys1 ,sys2);
Change sign of transfer function since the
%
disturbance has negative sign in the diagram.
sys_o=-sys_o •*
%
[yo,T]=step(sys_o); ^ Compute response to
step disturbance.
plot{T,yo)
title('Open-Loop Disturbance Slep Response')
FIGURE 4.29 xlabel(Time (s)'),ylabel('\omega_o'), grid
Analysis of the %
open-loop speed yo(length(T)) 4 Steady-state error —• last value of output yo.
control system.
(a) Response.
(b) m-file script. (b)
In a similar fashion, we begin the closed-loop system analysis by computing the
closed-loop transfer function from T (i(s) to (o(s) and then generating the time-
response of (o(t) to a unit step disturbance input. The output response and the
script cltach.m are shown in Figure 4.30. The closed-loop transfer function from the
disturbance input (from Equation (4.30)) is
- 1
T d(s) 2s + 541.5 sys_c.
As before, the steady-state error is just the final value of <o(t), which we denote by
w c(t) to indicate that it is a closed-loop. The steady-state error is shown on the plot in
Figure 4.30(a). We can obtain an approximate value of the steady-state error by look-
ing at the last value in the output vector y c, which we computed in the process of gen-
erating the plot in Figure 4.30(a). The approximate steady-state value of <o is
w c(oo) « <u f (0.02) = -0.002 rad/s.
We generally expect that <o c(oo)/a) 0(oo) < 0.02. In this example, the ratio of closed-
loop to open-loop steady-state speed output due to a unit step disturbance input is
(o c{oo)
= 0.003.
<*o{ OO)