Page 179 - Book Hosokawa Nanoparticle Technology Handbook

3.5 INTERACTIONS BETWEEN PARTICLES FUNDAMENTALS

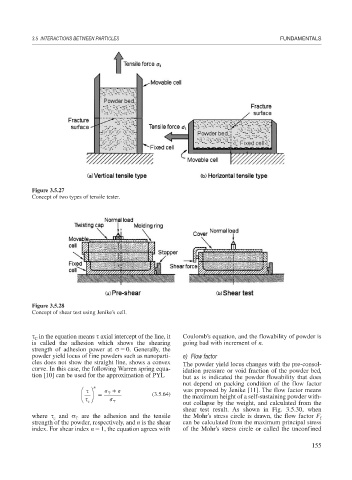
Figure 3.5.27
Concept of two types of tensile tester.

Figure 3.5.28
Concept of shear test using Jenike’s cell.

in the equation means axial intercept of the line, it Coulomb’s equation, and the flowability of powder is
C
is called the adhesion which shows the shearing going bad with increment of n.
strength of adhesion power at 0. Generally, the
powder yield locus of fine powders such as nanoparti- e) Flow factor
cles does not show the straight line, shows a convex The powder yield locus changes with the pre-consol-
curve. In this case, the following Warren spring equa- idation pressure or void fraction of the powder bed,
tion [10] can be used for the approximation of PYL but as is indicated the powder flowability that does
not depend on packing condition of the flow factor
⎛ ⎞ n was proposed by Jenike [11]. The flow factor means
⎜ ⎝ ⎠ ⎟ T T (3.5.64) the maximum height of a self-sustaining powder with-
c
out collapse by the weight, and calculated from the
shear test result. As shown in Fig. 3.5.30, when
where and are the adhesion and the tensile the Mohr’s stress circle is drawn, the flow factor F f
c
T
strength of the powder, respectively, and n is the shear can be calculated from the maximum principal stress
index. For shear index n 1, the equation agrees with of the Mohr’s stress circle or called the unconfined
155