Page 183 - Neural Network Modeling and Identification of Dynamical Systems

174 5. SEMIEMPIRICAL NEURAL NETWORK MODELS OF CONTROLLED DYNAMICAL SYSTEMS

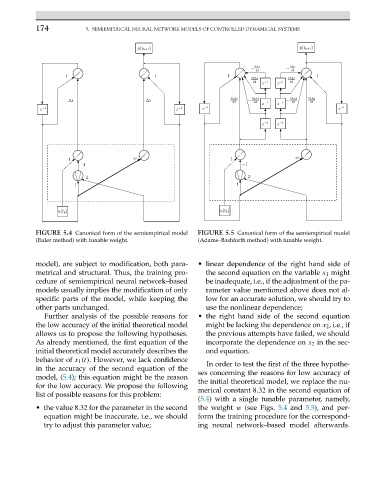
FIGURE 5.4 Canonical form of the semiempirical model FIGURE 5.5 Canonical form of the semiempirical model
(Euler method) with tunable weight. (Adams–Bashforth method) with tunable weight.

model), are subject to modification, both para- • linear dependence of the right hand side of
metrical and structural. Thus, the training pro- the second equation on the variable x 1 might
cedure of semiempirical neural network–based be inadequate, i.e., if the adjustment of the pa-
models usually implies the modification of only rameter value mentioned above does not al-
specific parts of the model, while keeping the low for an accurate solution, we should try to
other parts unchanged. use the nonlinear dependence;
Further analysis of the possible reasons for • the right hand side of the second equation
the low accuracy of the initial theoretical model might be lacking the dependence on x 2 , i.e., if
allows us to propose the following hypotheses. the previous attempts have failed, we should
As already mentioned, the first equation of the incorporate the dependence on x 2 in the sec-
initial theoretical model accurately describes the ond equation.
behavior of x 1 (t). However, we lack confidence
In order to test the first of the three hypothe-
in the accuracy of the second equation of the
ses concerning the reasons for low accuracy of
model, (5.4); this equation might be the reason
the initial theoretical model, we replace the nu-
for the low accuracy. We propose the following
merical constant 8.32 in the second equation of
list of possible reasons for this problem:
(5.4) with a single tunable parameter, namely,
• the value 8.32 for the parameter in the second the weight w (see Figs. 5.4 and 5.5), and per-
equation might be inaccurate, i.e., we should form the training procedure for the correspond-
try to adjust this parameter value; ing neural network–based model afterwards.