Page 185 - Neural Network Modeling and Identification of Dynamical Systems

176 5. SEMIEMPIRICAL NEURAL NETWORK MODELS OF CONTROLLED DYNAMICAL SYSTEMS

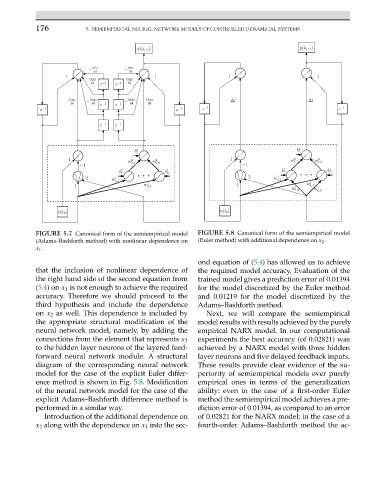
FIGURE 5.7 Canonical form of the semiempirical model FIGURE 5.8 Canonical form of the semiempirical model
(Adams–Bashforth method) with nonlinear dependence on (Euler method) with additional dependence on x 2 .
x 1 .
ondequationof(5.4) has allowed us to achieve
that the inclusion of nonlinear dependence of the required model accuracy. Evaluation of the
the right hand side of the second equation from trained model gives a prediction error of 0.01394
(5.4)on x 1 is not enough to achieve the required for the model discretized by the Euler method
accuracy. Therefore we should proceed to the and 0.01219 for the model discretized by the
third hypothesis and include the dependence Adams–Bashforth method.
on x 2 as well. This dependence is included by Next, we will compare the semiempirical
the appropriate structural modification of the model results with results achieved by the purely
neural network model, namely, by adding the empirical NARX model. In our computational
experiments the best accuracy (of 0.02821)was
connections from the element that represents x 2
to the hidden layer neurons of the layered feed- achieved by a NARX model with three hidden
forward neural network module. A structural layer neurons and five delayed feedback inputs.
diagram of the corresponding neural network These results provide clear evidence of the su-
model for the case of the explicit Euler differ- periority of semiempirical models over purely
ence method is shown in Fig. 5.8. Modification empirical ones in terms of the generalization
of the neural network model for the case of the ability: even in the case of a first-order Euler
explicit Adams–Bashforth difference method is method the semiempirical model achieves a pre-
performed in a similar way. diction error of 0.01394, as compared to an error
Introduction of the additional dependence on of 0.02821 for the NARX model; in the case of a
x 2 along with the dependence on x 1 into the sec- fourth-order Adams–Bashforth method the ac-