Page 219 - Numerical Analysis Using MATLAB and Excel

Chapter 6 Fourier, Taylor, and Maclaurin Series

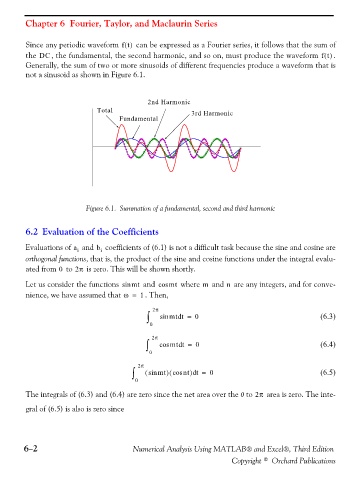
Since any periodic waveform ft() can be expressed as a Fourier series, it follows that the sum of
the DC , the fundamental, the second harmonic, and so on, must produce the waveform ft() .
Generally, the sum of two or more sinusoids of different frequencies produce a waveform that is
not a sinusoid as shown in Figure 6.1.

2nd Harmonic
Total 3rd Harmonic
3 Fundamental

2
1
0
-1
-2
-3
0 2 4 6 8 10 12

Figure 6.1. Summation of a fundamental, second and third harmonic

6.2 Evaluation of the Coefficients

Evaluations of and coefficients of (6.1) is not a difficult task because the sine and cosine are
a
b
i
i
orthogonal functions, that is, the product of the sine and cosine functions under the integral evalu-
ated from to 2π is zero. This will be shown shortly.
0
m
n
Let us consider the functions sin mt and cos mt where and are any integers, and for conve-
nience, we have assumed that ω = 1 . Then,
2π
∫ sin mt t = 0 (6.3)
d
0
2π
∫ cos mt t = 0 (6.4)
d
0
2π
∫ ( sin mt cos nt td = 0 (6.5)
(
)
)
0
The integrals of (6.3) and (6.4) are zero since the net area over the 0 to 2π area is zero. The inte-
gral of (6.5) is also is zero since

6−2 Numerical Analysis Using MATLAB® and Excel®, Third Edition
Copyright © Orchard Publications