Page 309 - Numerical Analysis Using MATLAB and Excel

Interpolation with MATLAB

%
% Use the following five statements to obtain |Z| versus radian frequency w
w=300:100:3000;
z=zeros(28,2);
z(:,1)=w';
z(:,2)=(10+(10.^4−j.*10.^6./w)./(10+j.*(0.1.*w−10.^5./w)))';
fprintf('%2.0f\t %10.3f\n',abs(z)')
%
w=[300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500....
1600 1700 1800 1900 2000 2100 2200 2300....
2400 2500 2600 2700 2800 2900 3000];
z=[39.339 52.789 71.104 97.665 140.437 222.182 436.056 1014.938...
469.830 266.032 187.052 145.751 120.353...
103.111 90.603 81.088 73.588 67.513 62.481...
58.240 54.611 51.468 48.717 46.286 44.122...
42.182 40.432 38.845];
semilogx(w,z); grid;
title('Magnitude of Impedance vs. Radian Frequency');
xlabel('w in rads/sec'); ylabel('|Z| in Ohms');
%
zi=interp1(w,z,792,'spline');
fprintf(' \n')
fprintf('Magnitude of Z at w=792 rad/s is %6.3f Ohms \n', zi)
fprintf(' \n')
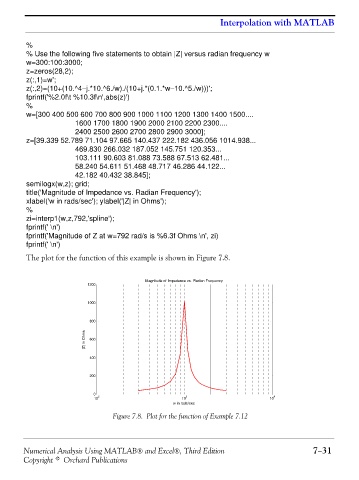
The plot for the function of this example is shown in Figure 7.8.

Magnitude of Impedance vs. Radian Frequency
1200

1000

800
|Z| in Ohms 600

400

200

0
2 3 4
10 10 10
w in rads/sec
Figure 7.8. Plot for the function of Example 7.12

Numerical Analysis Using MATLAB® and Excel®, Third Edition 7−31
Copyright © Orchard Publications