Page 59 - Numerical Analysis Using MATLAB and Excel

Chapter 2 Root Approximations

30

20

10

0

-10
-4 -3 -2 -1 0 1 2 3 4
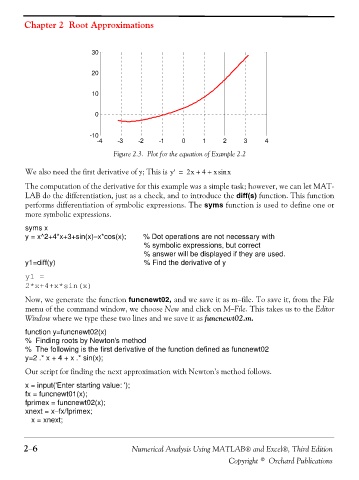
Figure 2.3. Plot for the equation of Example 2.2

We also need the first derivative of y; This is y' = 2x ++ xsin x
4
The computation of the derivative for this example was a simple task; however, we can let MAT-
LAB do the differentiation, just as a check, and to introduce the diff(s) function. This function
performs differentiation of symbolic expressions. The syms function is used to define one or
more symbolic expressions.

syms x
y = x^2+4*x+3+sin(x)−x*cos(x); % Dot operations are not necessary with
% symbolic expressions, but correct
% answer will be displayed if they are used.
y1=diff(y) % Find the derivative of y

y1 =
2*x+4+x*sin(x)
Now, we generate the function funcnewt02, and we save it as m−file. To save it, from the File
menu of the command window, we choose New and click on M−File. This takes us to the Editor
Window where we type these two lines and we save it as funcnewt02.m.

function y=funcnewt02(x)
% Finding roots by Newton's method
% The following is the first derivative of the function defined as funcnewt02
y=2 .* x + 4 + x .* sin(x);
Our script for finding the next approximation with Newton’s method follows.

x = input('Enter starting value: ');
fx = funcnewt01(x);
fprimex = funcnewt02(x);
xnext = x−fx/fprimex;
x = xnext;

2−6 Numerical Analysis Using MATLAB® and Excel®, Third Edition
Copyright © Orchard Publications