Page 125 - Partition & Adsorption of Organic Contaminants in Environmental Systems

116 CONTAMINANT SORPTION TO SOILS AND NATURAL SOLIDS

B
T 1 T 2
Soil Uptake, Q A

0
0 C (A,T ) C (A,T ) C (B,T ) C (B,T )
1
1
e
e
e
2
e
2
Equilibrium Concentration, C
e
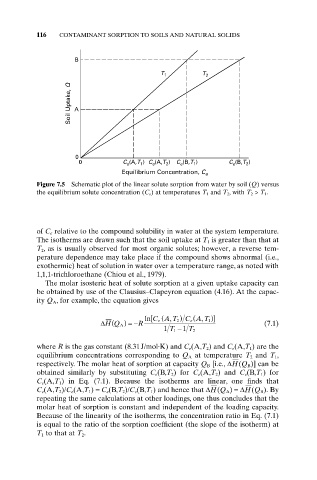
Figure 7.5 Schematic plot of the linear solute sorption from water by soil (Q) versus
the equilibrium solute concentration (C e ) at temperatures T 1 and T 2 , with T 2 > T 1 .
of C e relative to the compound solubility in water at the system temperature.
The isotherms are drawn such that the soil uptake at T 1 is greater than that at
T 2, as is usually observed for most organic solutes; however, a reverse tem-
perature dependence may take place if the compound shows abnormal (i.e.,
exothermic) heat of solution in water over a temperature range, as noted with
1,1,1-trichloroethane (Chiou et al., 1979).
The molar isosteric heat of solute sorption at a given uptake capacity can
be obtained by use of the Clausius–Clapeyron equation (4.16). At the capac-
ity Q A, for example, the equation gives

ln [ CA T ) C A T )]
e ( ,
e ( ,
1
2
(
DHQ A ) =- R (7.1)
1 T - 1 T 2
1
where R is the gas constant (8.31J/mol·K) and C e (A,T 2 ) and C e (A,T 1 ) are the
equilibrium concentrations corresponding to Q A at temperature T 2 and T 1,
respectively. The molar heat of sorption at capacity Q B [i.e., D (Q B)] can be
H
obtained similarly by substituting C e(B,T 2) for C e(A,T 2) and C e(B,T 1) for
C e(A,T 1) in Eq. (7.1). Because the isotherms are linear, one finds that
H
H
C e(A,T 2)/C e(A,T 1) = C e(B,T 2)/C e(B,T 1) and hence that D (Q A) =D (Q B). By
repeating the same calculations at other loadings, one thus concludes that the
molar heat of sorption is constant and independent of the loading capacity.
Because of the linearity of the isotherms, the concentration ratio in Eq. (7.1)
is equal to the ratio of the sorption coefficient (the slope of the isotherm) at
T 1 to that at T 2.