Page 170 - Probability Demystified

CHAPTER 9 The Normal Distribution 159

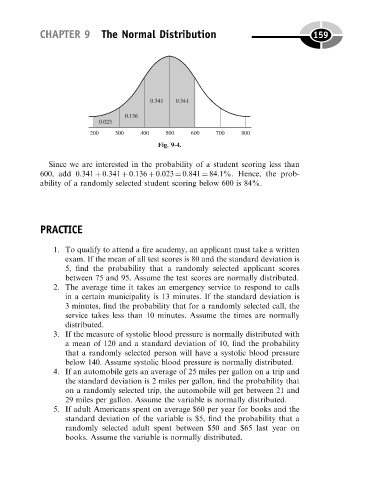
Fig. 9-4.

Since we are interested in the probability of a student scoring less than
600, add 0.341 þ 0.341 þ 0.136 þ 0.023 ¼ 0.841 ¼ 84.1%. Hence, the prob-
ability of a randomly selected student scoring below 600 is 84%.

PRACTICE

1. To qualify to attend a fire academy, an applicant must take a written
exam. If the mean of all test scores is 80 and the standard deviation is
5, find the probability that a randomly selected applicant scores
between 75 and 95. Assume the test scores are normally distributed.
2. The average time it takes an emergency service to respond to calls
in a certain municipality is 13 minutes. If the standard deviation is
3 minutes, find the probability that for a randomly selected call, the
service takes less than 10 minutes. Assume the times are normally
distributed.
3. If the measure of systolic blood pressure is normally distributed with
a mean of 120 and a standard deviation of 10, find the probability
that a randomly selected person will have a systolic blood pressure
below 140. Assume systolic blood pressure is normally distributed.
4. If an automobile gets an average of 25 miles per gallon on a trip and
the standard deviation is 2 miles per gallon, find the probability that
on a randomly selected trip, the automobile will get between 21 and
29 miles per gallon. Assume the variable is normally distributed.
5. If adult Americans spent on average $60 per year for books and the
standard deviation of the variable is $5, find the probability that a
randomly selected adult spent between $50 and $65 last year on
books. Assume the variable is normally distributed.