Page 247 - Process Equipment and Plant Design Principles and Practices by Subhabrata Ray Gargi Das

9.3 Representation of equilibrium 247

The simplest adsorption isotherm expresses loading (q) as proportional to fluid phase concentration,
resulting in an expression similar to Henry’s law.

q ¼ b c (9.5)
Isotherm equations
c is the equilibrium concentration of the solute in the mixture.

There are three commonly used mathematical expressions e
Langmuir, BET (BrunauereEmmetteTeller), and Freundlich isotherms to describe vapor/gas
adsorption equilibria as q vs p , the equilibrium partial pressure.

Table 9.4 provides the details of the equations.

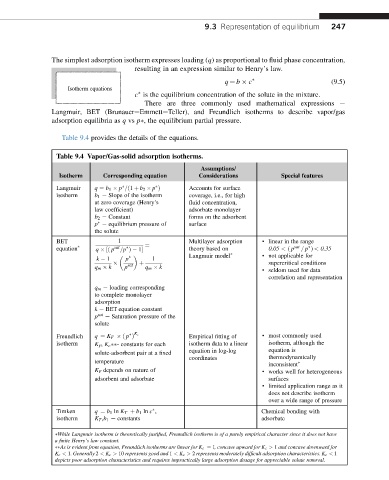
Table 9.4 Vapor/Gas-solid adsorption isotherms.
Assumptions/
Isotherm Corresponding equation Considerations Special features
Langmuir q ¼ b 1 p =ð1 þ b 2 p Þ Accounts for surface

isotherm b 1 e Slope of the isotherm coverage, i.e., for high
at zero coverage (Henry’s fluid concentration,
law coefficient) adsorbate monolayer
b 2 e Constant forms on the adsorbent
p e equilibrium pressure of surface

the solute
BET 1 Multilayer adsorption · linear in the range
equation sat ¼ theory based on 0.05 < ð p sat = p Þ < 0.35

q ½ð p =p Þ 1Š
Langmuir model · not applicable for
k 1 p 1

q m k p sat þ q m k supercritical conditions
· seldom used for data
correlation and representation
q m e loading corresponding
to complete monolayer
adsorption
k e BET equation constant
p sat e Saturation pressure of the
solute
K c
Freundlich q ¼ K F ð p Þ Empirical fitting of · most commonly used
isotherm K F , K c - constants for each isotherm data to a linear isotherm, although the
equation in log-log equation is
solute-adsorbent pair at a fixed
coordinates thermodynamically
temperature
inconsistent
K F depends on nature of
· works well for heterogeneous
adsorbent and adsorbate surfaces
· limited application range as it
does not describe isotherm
over a wide range of pressure
Timken q ¼ b 1 ln K T þ b 1 ln c , Chemical bonding with

isotherm K T ,b 1 e constants adsorbate
While Langmuir isotherm is theoretically justified, Freundlich isotherm is of a purely empirical character since it does not have
a finite Henry’s law constant.
As is evident from equation, Freundlich isotherms are linear for K c ¼ 1, concave upward for K c > 1 and concave downward for
K c < 1. Generally 2 < K c > 10 represents good and 1 < K c > 2 represents moderately difficult adsorption characteristics. K c < 1
depicts poor adsorption characteristics and requires impractically large adsorption dosage for appreciable solute removal.