Page 184 - Schaum's Outline of Theory and Problems of Advanced Calculus

CHAP. 7] VECTORS 175

2
2
2
2
2
2
2
2
2
and ðdsÞ ¼ðdxÞ þðdyÞ þðdzÞ ¼ðdrÞ þ r ðd Þ þ r sin ðd Þ 2
The scale factors are h 1 ¼ h r ¼ 1; h 2 ¼ h ¼ r; h 3 ¼ h ¼ r sin .
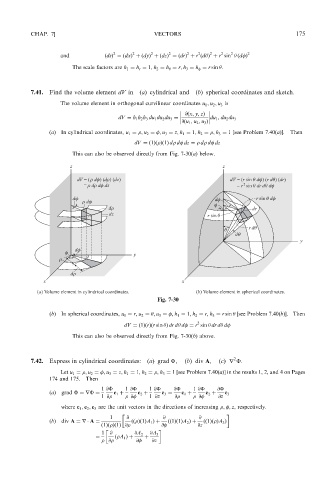
7.41. Find the volume element dV in (a) cylindrical and (b) spherical coordinates and sketch.
The volume element in orthogonal curvilinear coordinates u 1 ; u 2 ; u 3 is

@ðx; y; zÞ

dV ¼ h 1 h 2 h 3 du 1 du 2 du 3 ¼ du 1 ; du 2 du 3

@ðu 1 ; u 2 ; u 3 Þ
(a)Incylindrical coordinates, u 1 ¼ ; u 2 ¼ ; u 3 ¼ z; h 1 ¼ 1; h 2 ¼ ; h 3 ¼ 1 [see Problem 7.40(a)]. Then
dV ¼ð1Þð Þð1Þ d d dz ¼ d d dz
This can also be observed directly from Fig. 7-30(a)below.

Fig. 7-30

(b)Inspherical coordinates, u 1 ¼ r; u 2 ¼ ; u 3 ¼ ; h 1 ¼ 1; h 2 ¼ r; h 3 ¼ r sin [see Problem 7.40(b)]. Then
2
dV ¼ð1ÞðrÞðr sin Þ dr d d ¼ r sin dr d d
This can also be observed directly from Fig. 7-30(b) above.

2
7.42. Express in cylindrical coordinates: (a) grad ; ðbÞ div A; ðcÞr .
Let u 1 ¼ ; u 2 ¼ ; u 3 ¼ z; h 1 ¼ 1; h 2 ¼ ; h 3 ¼ 1 [see Problem 7.40(a)] in the results 1, 2, and 4 on Pages
174 and 175. Then
1 @ 1 @ 1 @ @ 1 @ @
e 3
ðaÞ grad ¼r ¼ e 1 þ e 2 þ e 3 ¼ e 1 þ e 2 þ
1 @ @ 1 @z @ @ @z
where e 1 ; e 2 ; e 3 are the unit vectors in the directions of increasing ; ; z, respectively.

1 @ @ @
ð1Þð Þð1Þ @ @ @z
ðbÞ div A ¼r A ¼ ð ð Þð1ÞA 1 Þ þ ðð1Þð1ÞA 2 Þþ ðð1Þð ÞA 3 Þ
1 @ @A 2 @A 3

@ @ @z
¼ ð A 1 Þþ þ