Page 287 - Semiconductor For Micro- and Nanotechnology An Introduction For Engineers

Interacting Subsystems
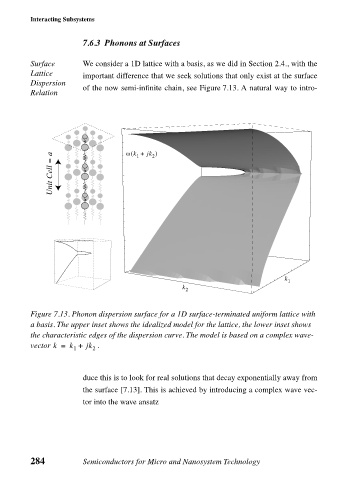
We consider a 1D lattice with a basis, as we did in Section 2.4., with the
Surface 7.6.3 Phonons at Surfaces
Lattice important difference that we seek solutions that only exist at the surface
Dispersion
of the now semi-infinite chain, see Figure 7.13. A natural way to intro-
Relation

(
Unit Cell = a ω k + jk )
1
2

k
1
k
2
Figure 7.13. Phonon dispersion surface for a 1D surface-terminated uniform lattice with
a basis. The upper inset shows the idealized model for the lattice, the lower inset shows
the characteristic edges of the dispersion curve. The model is based on a complex wave-
vector k = k + jk .
1 2

duce this is to look for real solutions that decay exponentially away from
the surface [7.13]. This is achieved by introducing a complex wave vec-
tor into the wave ansatz

284 Semiconductors for Micro and Nanosystem Technology