Page 131 - Separation process principles 2

96 Chapter 3 Mass Transfer and Diffusion

The entry length to achieve fully developed flow is de- The Graetz solution of (3-147) for the temperature profile
fined as the axial distance, L,, from the entrance to the point or the concentration profile is in the form of an infinite
at which the centerline velocity is 99% of the fully devel- series, and can be obtained from (3-146) by the method of
oped flow value. From the analysis of Langhaar [43] for the separation of variables using the method of Frobenius. A
entry region, detailed solution is given by Sellars, Tribus, and Klein [45].
From the concentration profile, expressions for the mass-
transfer coefficient and the Sherwood number are obtained.
When x is large, the concentration profile is fully developed
Thus, at the upper limit of laminar flow, NR, = 2,100, L,/D = and the local Sherwood number, Nshx, approaches a limiting
12 1, a rather large ratio. For NRe = 100, the ratio is only 5.75. value of 3.656. At the other extreme, when x is small such
In the entry region, Langhaar's analysis shows the friction fac- that the concentration boundary layer is very thin and con-
tor is considerably higher than the fully developed flow value fined to a region where the fully developed velocity profile is
given by (3-144). At x = 0, f is infinity, but then decreases ex- linear, the local Sherwood number is obtained from the
ponentially withx, approaching the fully developed flow value classic Leveque [46] solution, presented by Knudsen and
at L,. For example, for NRe = 1,000, (3-144) gives f = 0.016, Katz [47]:
with L,/D = 57.5. In the region fromx = 0 tox/D = 5.35, the
average friction factor from Langhaar is 0.0487, which is
about three times higher than the fully developed value.
In 1885, Graetz [44] obtained a theoretical solution to
the problem of convective heat transfer between the wall of where
a circular tube, held at a constant temperature, and a fluid
flowing through the tube in fully developed laminar flow.
Assuming constant properties and negligible conduction in
the axial direction, the energy equation, after substituting
(3-140) for u,, is
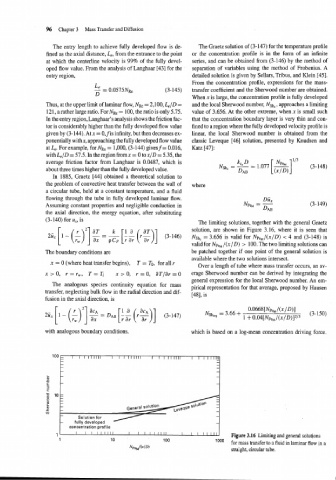
The limiting solutions, together with the general Graetz
solution, are shown in Figure 3.16, where it is seen that
NShx = 3.656 is valid for NpeM/(x/D) < 4 and (3-148) is
valid for NpeM /(XI D) > 100. The two limiting solutions can
The boundary conditions are be patched together if one point of the general solution is
available where the two solutions intersect.
x = 0 (where heat transfer begins), T = To, for all r
Over a length of tube where mass transfer occurs, an av-
erage Sherwood number can be derived by integrating the
general expression for the local Sherwood number. An em-
The analogous species continuity equation for mass
pirical representation for that average, proposed by Hausen
transfer, neglecting bulk flow in the radial direction and dif-
[48], is
fusion in the axial direction, is

with analogous boundary conditions. which is based on a log-mean concentration driving force.

V)
fullv develooed
( concentration profile I
11 I 1 1 1 1 1 1 1 1 I 1 1 1 1 1 1 1 1 I I 1 1 1 1 1 1 1 Figure 3.16 Limiting and general solutions
1 10 100 looO
for mass transfer to a fluid in laminar flow in a
NPeM/(xID)
straight, circular tube.