Page 135 - Separation process principles 2

100 Chapter 3 Mass Transfer and Diffusion

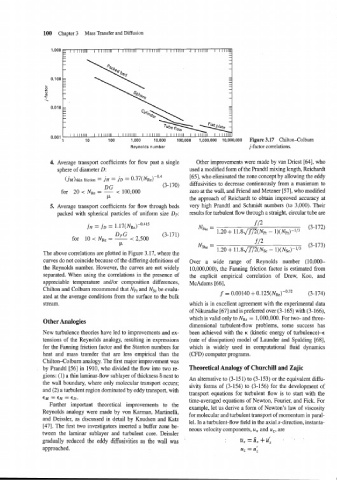
Figure 3.17 Chilton-Colburn
Reynolds number j-factor correlations.

4. Average transport coefficients for flow past a single Other improvements were made by van Driest [64], who
sphere of diameter D: used a modified form of the Prandtl mixing length, Reichardt
[65], who eliminated the zone concept by allowing the eddy
(j~)skin friction = j~ = j~ = O.~~(NR~)-O.~
diffusivities to decrease continuously from a maximum to
DG (3-170)
for 20 < NRe = - < 100,000 zero at the wall, and Friend and Metzner [57], who modified
P the approach of Reichardt to obtain improved accuracy at
5. Average transport coefficients for flow through beds very high Prandtl and Schmidt numbers (to 3,000). Their
packed with spherical particles of uniform size Dp: results for turbulent flow through a straight, circular tube are
-0.415
jH = jD = 1.17(NRe) f 12 (3-172)
N~tH =
(3-171) 1.20 + 1 1.8m(Np, - l)(Npr)-'I3
for 10<NRe=- DPG < 2,500
P N~tM = f 12 (3-173)
1.20 + 1 1.8m(Nsc - l)(Nsc)-'I3
The above correlations are plotted in Figure 3.17, where the
curves do not coincide because of the differing definitions of Over a wide range of Reynolds number (10,000-
the Reynolds umber. However, the curves are not widely 10,000,000), the Fanning friction factor is estimated from
separated. When using the correlations in the presence of the explicit empirical correlation of Drew, Koo, and
appreciable temperature and/or composition differences, McAdams [66],
Chilton and Colburn recommend that Np, and Ns, be evalu-
(3-174)
f = 0.00140 + 0.125(~~~)-"~~
ated at the average conditions from the surface to the bulk
stream. which is in excellent agreement with the experimental data
of Nikuradse [67] and is preferred over (3-165) with (3- 166),
which is valid only to NRe = 1,000,000. For two- and three-
Other Analogies
dimensional turbulent-flow problems, some success has
New turbulence theories have led to improvements and ex- been achieved with the K (kinetic energy of turbulence)+
tensions of the Reynolds analogy, resulting in expressions (rate of dissipation) model of Launder and Spalding [68],
for the Fanning friction factor and the Stanton numbers for which is widely used in computational fluid dynamics
heat and mass transfer that are less empirical than the (CFD) computer programs.
Chilton-Colburn analogy. The first major improvement was
by Prandtl [56] in 1910, who divided the flow into two re- Theoretical Analogy of Churchill and Zajic
gions: (1) a thin laminar-flow sublayer thickness next to
An alternative to (3-151) to (3-153) or the equivalent diffu-
the wall boundary, where Occurs; sivity forms of (3-154) to (3-156) for the development of
and (2) aturbulent region with
trans~ort eauations for turbulent flow is to start with the
EM =EH =ED.
time-averaged equations of Newton, Fourier, and Fick. For
to the
example, let us derive a form of Newton's law of viscosity
were made by 'On Manine11i9 for molecular and turbulent transport of momentum in paral-
and Deissler, as discussed in by 'Iludsen and Katz lel. In a turbulent-flow field in the axial >direction, instanta-
[47]. The first two investigators inserted a buffer zone be-
neous velocity components, ux and uz, are
tween the laminar sublaver and turbulent core. Deissler
gradually reduced the eddy diffusivities as the wall was uX=Ux+u~ , , .
approached.
U, = U: