Page 149 - Shigley's Mechanical Engineering Design

bud29281_ch03_071-146.qxd 11/24/09 3:02PM Page 124 ntt 203:MHDQ196:bud29281:0073529281:bud29281_pagefiles:

124 Mechanical Engineering Design
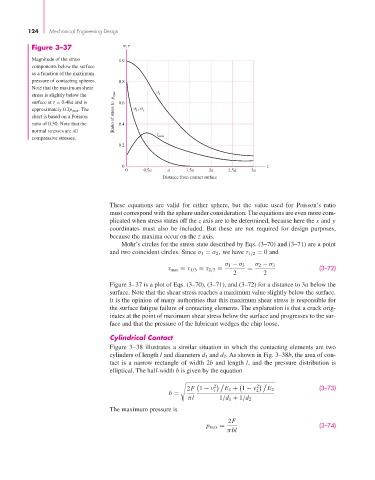
Figure 3–37 ,

Magnitude of the stress 1.0
components below the surface
as a function of the maximum
pressure of contacting spheres. 0.8
Note that the maximum shear
stress is slightly below the z
surface at z = 0.48a and is 0.6
approximately 0.3p max . The Ratio of stress to p max , y
x
chart is based on a Poisson
ratio of 0.30. Note that the 0.4
normal stresses are all
compressive stresses. max
0.2

0 z
0 0.5a a 1.5a 2a 2.5a 3a
Distance from contact surface

These equations are valid for either sphere, but the value used for Poisson’s ratio
must correspond with the sphere under consideration. The equations are even more com-
plicated when stress states off the z axis are to be determined, because here the x and y
coordinates must also be included. But these are not required for design purposes,
because the maxima occur on the z axis.
Mohr’s circles for the stress state described by Eqs. (3–70) and (3–71) are a point
and two coincident circles. Since σ 1 = σ 2 , we have τ 1/2 = 0 and
σ 1 − σ 3 σ 2 − σ 3
τ max = τ 1/3 = τ 2/3 = = (3–72)
2 2
Figure 3–37 is a plot of Eqs. (3–70), (3–71), and (3–72) for a distance to 3a below the
surface. Note that the shear stress reaches a maximum value slightly below the surface.
It is the opinion of many authorities that this maximum shear stress is responsible for
the surface fatigue failure of contacting elements. The explanation is that a crack orig-
inates at the point of maximum shear stress below the surface and progresses to the sur-
face and that the pressure of the lubricant wedges the chip loose.
Cylindrical Contact
Figure 3–38 illustrates a similar situation in which the contacting elements are two
cylinders of length l and diameters d 1 and d 2. As shown in Fig. 3–38b, the area of con-
tact is a narrow rectangle of width 2b and length l, and the pressure distribution is
elliptical. The half-width b is given by the equation

2 2
2F 1 − ν 1 E 1 + 1 − ν 2 E 2 (3–73)
b =
πl 1/d 1 + 1/d 2
The maximum pressure is
2F
p max = (3–74)
πbl