Page 151 - Shigley's Mechanical Engineering Design

bud29281_ch03_071-146.qxd 11/24/09 3:02PM Page 126 ntt 203:MHDQ196:bud29281:0073529281:bud29281_pagefiles:

126 Mechanical Engineering Design
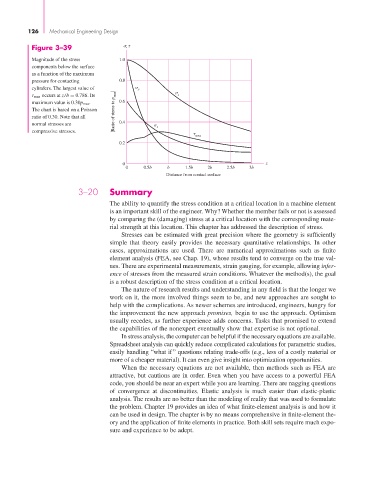
Figure 3–39 ,

Magnitude of the stress 1.0
components below the surface
as a function of the maximum
pressure for contacting 0.8
cylinders. The largest value of y
max occurs at z/b = 0.786. Its z
maximum value is 0.30p max . 0.6
The chart is based on a Poisson Ratio of stress to p max
ratio of 0.30. Note that all
normal stresses are 0.4 x
compressive stresses.
max
0.2

0 z
0 0.5b b 1.5b 2b 2.5b 3b
Distance from contact surface

3–20 Summary
The ability to quantify the stress condition at a critical location in a machine element
is an important skill of the engineer. Why? Whether the member fails or not is assessed
by comparing the (damaging) stress at a critical location with the corresponding mate-
rial strength at this location. This chapter has addressed the description of stress.
Stresses can be estimated with great precision where the geometry is sufficiently
simple that theory easily provides the necessary quantitative relationships. In other
cases, approximations are used. There are numerical approximations such as finite
element analysis (FEA, see Chap. 19), whose results tend to converge on the true val-
ues. There are experimental measurements, strain gauging, for example, allowing infer-
ence of stresses from the measured strain conditions. Whatever the method(s), the goal
is a robust description of the stress condition at a critical location.
The nature of research results and understanding in any field is that the longer we
work on it, the more involved things seem to be, and new approaches are sought to
help with the complications. As newer schemes are introduced, engineers, hungry for
the improvement the new approach promises, begin to use the approach. Optimism
usually recedes, as further experience adds concerns. Tasks that promised to extend
the capabilities of the nonexpert eventually show that expertise is not optional.
In stress analysis, the computer can be helpful if the necessary equations are available.
Spreadsheet analysis can quickly reduce complicated calculations for parametric studies,
easily handling “what if” questions relating trade-offs (e.g., less of a costly material or
more of a cheaper material). It can even give insight into optimization opportunities.
When the necessary equations are not available, then methods such as FEA are
attractive, but cautions are in order. Even when you have access to a powerful FEA
code, you should be near an expert while you are learning. There are nagging questions
of convergence at discontinuities. Elastic analysis is much easier than elastic-plastic
analysis. The results are no better than the modeling of reality that was used to formulate
the problem. Chapter 19 provides an idea of what finite-element analysis is and how it
can be used in design. The chapter is by no means comprehensive in finite-element the-
ory and the application of finite elements in practice. Both skill sets require much expo-
sure and experience to be adept.