Page 89 - Shigley's Mechanical Engineering Design

bud29281_ch02_031-070.qxd 11/12/2009 8:00 pm Page 64 pinnacle s-171:Desktop Folder:Temp Work:Don't Delete (Jobs):MHDQ196/Budynas:

64 Mechanical Engineering Design
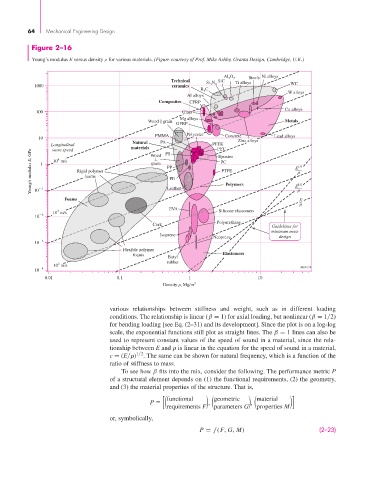
Figure 2–16

Young’s modulus E versus density ρ for various materials. (Figure courtesy of Prof. Mike Ashby, Granta Design, Cambridge, U.K.)

Al O 3 Steels Ni alloys
2
Technical Si N SiC Ti alloys
1000 ceramics 3 4 WC
B 4 C W alloys
Al alloys
Composites CFRP
Cu alloys
100 Glass
Mg alloys
Wood || grain GFRP Metals
10 PMMA Polyester Concrete Lead alloys
Natural PA Zinc alloys
Longitudinal materials Wood PS PEEK
PET
wave speed
Young's modulus E, GPa 1 10 m/s Rigid polymer grain PP PE PC Polymers E 1/3
Epoxies
⊥
4
PTFE
foams
1/2
1
10
Foams Leather E E

3 EVA Silicone elastomers
10 m/s
10 2
Cork Polyurethane
Guidelines for
minimum mass
Isoprene
Neoprene design
10 3
Flexible polymer
foams Butyl Elastomers
2 rubber
10 m/s MFA C4
10 4
0.01 0.1 1 10
Density , Mg/m 3
various relationships between stiffness and weight, such as in different loading
conditions. The relationship is linear (β = 1) for axial loading, but nonlinear (β = 1 2)
for bending loading [see Eq. (2–31) and its development]. Since the plot is on a log-log
scale, the exponential functions still plot as straight lines. The β = 1 lines can also be
used to represent constant values of the speed of sound in a material, since the rela-
tionship between E and r is linear in the equation for the speed of sound in a material,
c = (E r) 1 2 . The same can be shown for natural frequency, which is a function of the
ratio of stiffness to mass.
To see how β fits into the mix, consider the following. The performance metric P
of a structural element depends on (1) the functional requirements, (2) the geometry,
and (3) the material properties of the structure. That is,
[( functional geometric ( ) material )]
) (
P requirements F , parameters G properties M

,
or, symbolically,
P = f (F, G, M) (2–23)