Page 164 - Statistics for Environmental Engineers

L1592_frame_C19.fm Page 162 Tuesday, December 18, 2001 1:53 PM

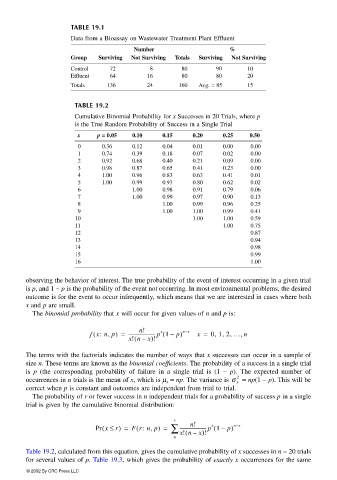
TABLE 19.1
Data from a Bioassay on Wastewater Treatment Plant Effluent
Number %
Group Surviving Not Surviving Totals Surviving Not Surviving
Control 72 8 80 90 10
Effluent 64 16 80 80 20
Totals 136 24 160 Avg. = 85 15

TABLE 19.2
Cumulative Binomial Probability for x Successes in 20 Trials, where p
is the True Random Probability of Success in a Single Trial
x p == == 0.05 0.10 0.15 0.20 0.25 0.50
0 0.36 0.12 0.04 0.01 0.00 0.00
1 0.74 0.39 0.18 0.07 0.02 0.00
2 0.92 0.68 0.40 0.21 0.09 0.00
3 0.98 0.87 0.65 0.41 0.23 0.00
4 1.00 0.96 0.83 0.63 0.41 0.01
5 1.00 0.99 0.93 0.80 0.62 0.02
6 1.00 0.98 0.91 0.79 0.06
7 1.00 0.99 0.97 0.90 0.13
8 1.00 0.99 0.96 0.25
9 1.00 1.00 0.99 0.41
10 1.00 1.00 0.59
11 1.00 0.75
12 0.87
13 0.94
14 0.98
15 0.99
16 1.00

observing the behavior of interest. The true probability of the event of interest occurring in a given trial
is p, and 1 − p is the probability of the event not occurring. In most environmental problems, the desired
outcome is for the event to occur infrequently, which means that we are interested in cases where both
x and p are small.
The binomial probability that x will occur for given values of n and p is:

n!
(
f x: n, p) = ----------------------- p 1 –( p) n−x x = 0, 1, 2, …, n
x
(
x! n – x)!
The terms with the factorials indicates the number of ways that x successes can occur in a sample of
size n. These terms are known as the binomial coefficients. The probability of a success in a single trial
is p (the corresponding probability of failure in a single trial is (1 − p). The expected number of
2
occurrences in n trials is the mean of x, which is µ x = np. The variance is σ x = np(1 − p). This will be
correct when p is constant and outcomes are independent from trial to trial.
The probability of r or fewer success in n independent trials for a probability of success p in a single
trial is given by the cumulative binomial distribution:

r
n!
x
(
Pr x ≤ r) = Fr: n, p) = ∑ ----------------------- p 1 –( p) n−x
(
(
0 x! n – x)!
Table 19.2, calculated from this equation, gives the cumulative probability of x successes in n = 20 trials
for several values of p. Table 19.3, which gives the probability of exactly x occurrences for the same
© 2002 By CRC Press LLC