Page 171 - Statistics for Environmental Engineers

L1592_Frame_C20 Page 170 Tuesday, December 18, 2001 1:53 PM

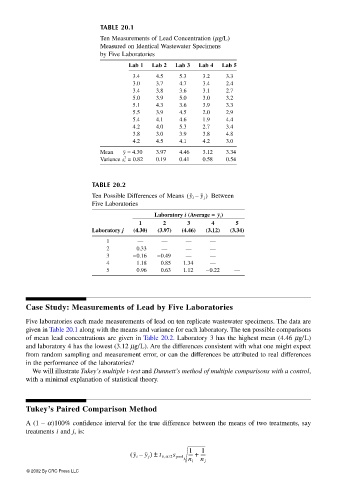
TABLE 20.1
Ten Measurements of Lead Concentration (µg/L)
Measured on Identical Wastewater Specimens
by Five Laboratories
Lab 1 Lab 2 Lab 3 Lab 4 Lab 5
3.4 4.5 5.3 3.2 3.3
3.0 3.7 4.7 3.4 2.4
3.4 3.8 3.6 3.1 2.7
5.0 3.9 5.0 3.0 3.2
5.1 4.3 3.6 3.9 3.3
5.5 3.9 4.5 2.0 2.9
5.4 4.1 4.6 1.9 4.4
4.2 4.0 5.3 2.7 3.4
3.8 3.0 3.9 3.8 4.8
4.2 4.5 4.1 4.2 3.0
Mean y = 4.30 3.97 4.46 3.12 3.34
2
Variance = 0.82 0.19 0.41 0.58 0.54
s i

TABLE 20.2
Ten Possible Differences of Means y i –( y j ) Between
Five Laboratories
y
Laboratory i (Average = ) i
1 2 3 4 5
Laboratory j (4.30) (3.97) (4.46) (3.12) (3.34)
1 — — — —
2 0.33 — — —
3 −0.16 −0.49 — —
4 1.18 0.85 1.34 —
5 0.96 0.63 1.12 −0.22 —

Case Study: Measurements of Lead by Five Laboratories
Five laboratories each made measurements of lead on ten replicate wastewater specimens. The data are
given in Table 20.1 along with the means and variance for each laboratory. The ten possible comparisons
of mean lead concentrations are given in Table 20.2. Laboratory 3 has the highest mean (4.46 µg/L)
and laboratory 4 has the lowest (3.12 µg/L). Are the differences consistent with what one might expect
from random sampling and measurement error, or can the differences be attributed to real differences
in the performance of the laboratories?
We will illustrate Tukey’s multiple t-test and Dunnett’s method of multiple comparisons with a control,
with a minimal explanation of statistical theory.

Tukey’s Paired Comparison Method

A (1 – α)100% confidence interval for the true difference between the means of two treatments, say
treatments i and j, is:

1
1
( y i – y j ) ± t ν,α /2 s pool ---- + ----
n i n j
© 2002 By CRC Press LLC