Page 1118 - The Mechatronics Handbook

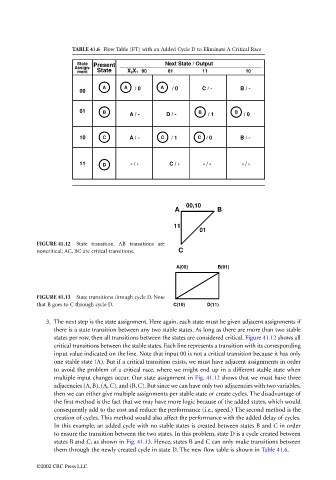
TABLE 41.6 Flow Table (FT) with an Added Cycle D to Eliminate A Critical Race

State Present Next State / Output
Assign-
ment State X 2X 1 00 01 11 10
A A / 0 A / 0 C / - B / -
00

01 B A / - D / - B / 1 B / 0

10 C A / - C / 1 C / 0 B / -

11 D - / - C / - - / - - / -

00,10
A B

11
01
FIGURE 41.12 State transition. AB transitions are
noncritical; AC, BC are critical transitions. C

A(00) B(01)

FIGURE 41.13 State transitions through cycle D. Note
that B goes to C through cycle D. C(10) D(11)

3. The next step is the state assignment. Here again, each state must be given adjacent assignments if
there is a state transition between any two stable states. As long as there are more than two stable
states per row, then all transitions between the states are considered critical. Figure 41.12 shows all
critical transitions between the stable states. Each line represents a transition with its corresponding
input value indicated on the line. Note that input 00 is not a critical transition because it has only
one stable state (A). But if a critical transition exists, we must have adjacent assignments in order
to avoid the problem of a critical race, where we might end up in a different stable state when
multiple input changes occur. Our state assignment in Fig. 41.12 shows that we must have three
adjacencies (A, B), (A, C), and (B, C). But since we can have only two adjacencies with two variables,
then we can either give multiple assignments per stable state or create cycles. The disadvantage of
the first method is the fact that we may have more logic because of the added states, which would
consequently add to the cost and reduce the performance (i.e., speed.) The second method is the
creation of cycles. This method would also affect the performance with the added delay of cycles.
In this example, an added cycle with no stable states is created between states B and C in order
to ensure the transition between the two states. In this problem, state D is a cycle created between
states B and C, as shown in Fig. 41.13. Hence, states B and C can only make transitions between
them through the newly created cycle in state D. The new flow table is shown in Table 41.6.

©2002 CRC Press LLC