Page 844 - The Mechatronics Handbook

0066_frame_C27 Page 5 Wednesday, January 9, 2002 7:10 PM

20
First—order pole factor 20 dB/dec
First—order zero factor
Magnitude (dB) −10 0 Asymptotic curves
10
−20 dB/dec
−20
90
45 deg/dec
45
Phase (deg) 0
−45
−45 deg/dec
−90
0.1/t 1/t 10/t
Frequency w
±1
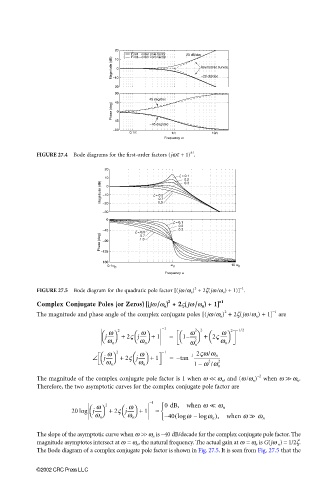
FIGURE 27.4 Bode diagrams for the first-order factors (jωτ + 1) .
20
z = 0.1
10 0.2
Magnitude (dB) −10 0 z = 0.5
0.3
0.7
−20
−30 1.0
0
z = 0.1
0.2
−45 z = 0.5 0.3
Phase (deg) −135 0.7
1.0
−90
−180

0.1w w n 10 w n
n

Frequency w
2
−1
FIGURE 27.5 Bode diagram for the quadratic pole factor [(jω /ω n ) + 2ζ(jω /ω n ) + 1)] .
±1
2
Complex Conjugate Poles (or Zeros) [(jω /ω n ) + 2ς( jω /ω n ) + 1]
−1
2
The magnitude and phase angle of the complex conjugate poles [(jω /ω n ) + 2ζ(jω /ω n ) + 1] are
– 1 2 2 2 – 1/2
2
w
 w  + 2V j------ + =  w  +  w 


–
 j------    1  1 ------ 2  2V ------ 
w n
w n
w n w n


w
w
∠   j------   2 + 2V j------ + 1 – 1 = – tan ----------------------- 2
–
1 2Vw/w n


2
–
w n
w n
1 w /w n
−2
The magnitude of the complex conjugate pole factor is 1 when ω << ω n , and (ω /ω n ) when ω >> ω n .
Therefore, the two asymptotic curves for the complex conjugate pole factor are
– 1
 w  2  w   0 dB, when w << w n
20 log  j------  + 2V j------ + 1 ≈ 


(
w n w n  – 40 log w – log w n ), when w > > w n
The slope of the asymptotic curve when ω >> ω n is −40 dB/decade for the complex conjugate pole factor. The
magnitude asymptotes intersect at ω = ω n , the natural frequency. The actual gain at ω = ω n is G(jω n ) = 1/2ζ.
The Bode diagram of a complex conjugate pole factor is shown in Fig. 27.5. It is seen from Fig. 27.5 that the
©2002 CRC Press LLC