Page 926 - The Mechatronics Handbook

0066_Frame_C30 Page 37 Thursday, January 10, 2002 4:44 PM

Target Open Loop Singular Values at Output
40

30

20
Singular Values (dB) 10

0

−10

−20
−1 0 1 2
10 10 10 10
Frequency (rad/sec)
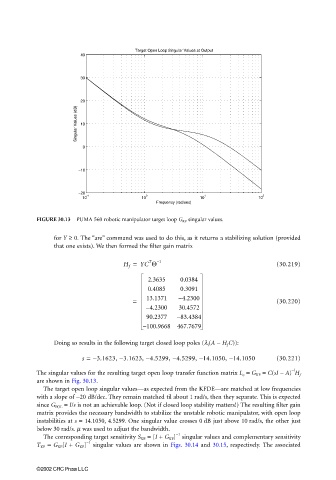
FIGURE 30.13 PUMA 560 robotic manipulator target loop G KF singular values.

for Y ≥ 0. The “are” command was used to do this, as it returns a stabilizing solution (provided
that one exists). We then formed the filter gain matrix

H f = YC Θ – 1 (30.219)
T
2.3635 0.0384
0.4085 0.3091
= 13.1371 – 4.2300 (30.220)
– 4.2300 30.4572
90.2377 – 83.4384
– 100.9668 467.7679

Doing so results in the following target closed loop poles (λ i (A − H f C)):

s = −3.1623, −3.1623, −4.5299, −4.5299, −14.1050, −14.1050 (30.221)

−l
The singular values for the resulting target open loop transfer function matrix L o = G KF = C(sI − A) H f
are shown in Fig. 30.13.
The target open loop singular values—as expected from the KFDE—are matched at low frequencies
with a slope of −20 dB/dec. They remain matched til about 1 rad/s, then they separate. This is expected
since G FOL = I/s is not an achievable loop. (Not if closed loop stability matters!) The resulting filter gain
matrix provides the necessary bandwidth to stabilize the unstable robotic manipulator, with open loop
instabilities at s = 14.1050, 4.5299. One singular value crosses 0 dB just above 10 rad/s, the other just
below 30 rad/s. µ was used to adjust the bandwidth.
−1
The corresponding target sensitivity S KF = [I + G KF ] singular values and complementary sensitivity
−1
T KF = G KF [I + G KF ] singular values are shown in Figs. 30.14 and 30.15, respectively. The associated

©2002 CRC Press LLC