Page 50 - Using ANSYS for Finite Element Analysis A Tutorial for Engineers

IntroductIon to FInIte element AnAlysIs • 37
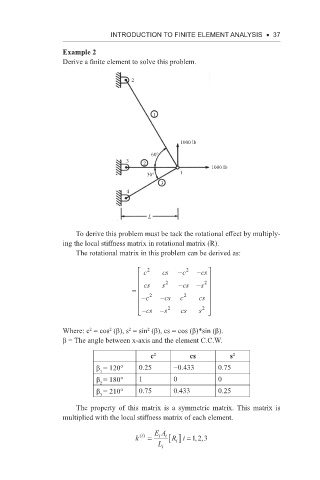
Example 2
Derive a finite element to solve this problem.

2

1

1000 lb
60°
3 2
1000 lb
30° 1
3
4

L

To derive this problem must be tack the rotational effect by multiply-
ing the local stiffness matrix in rotational matrix (R).
The rotational matrix in this problem can be derived as:

 c 2 cs −c 2 − 
cs
 2 2 
=  cs s −cs −s  

 −c 2 −cs c 2 cs 
 2 2 
 −cs −s cs s 

Where: c = cos (β), s = sin (β), cs = cos (β)*sin (β).
2
2
2
2
β = The angle between x-axis and the element C.C.W.
c 2 cs s 2
β = 120° 0.25 −0.433 0.75
1
β = 180° 1 0 0
2
β = 210° 0.75 0.433 0.25
3
The property of this matrix is a symmetric matrix. This matrix is
multiplied with the local stiffness matrix of each element.

EA
i []
k i () = ii Ri = 12
,,3
L i