Page 139 - Wind Energy Handbook

THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 113

1.5

F(µ)
1
F (µ)
φ
1
µ
2 0.5

0
0 0.25 0.5 0.75 1
µ

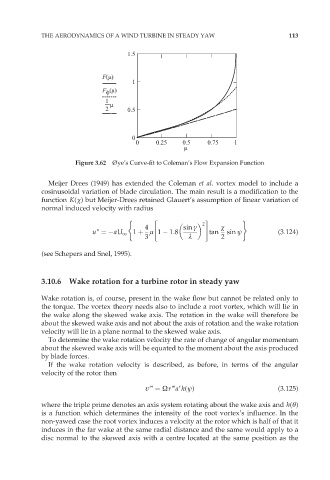
Figure 3.62 Øye’s Curve-fit to Coleman’s Flow Expansion Function

Meijer Drees (1949) has extended the Coleman et al. vortex model to include a
cosinusoidal variation of blade circulation. The main result is a modification to the
function K(÷) but Meijer-Drees retained Glauert’s assumption of linear variation of
normal induced velocity with radius
( " # )
4 sin ª 2 ÷
u0 ¼ aU 1 1 þ ì 1 1:8 tan sin ł (3:124)
3 º 2

(see Schepers and Snel, 1995).

3.10.6 Wake rotation for a turbine rotor in steady yaw

Wake rotation is, of course, present in the wake flow but cannot be related only to
the torque. The vortex theory needs also to include a root vortex, which will lie in
the wake along the skewed wake axis. The rotation in the wake will therefore be
about the skewed wake axis and not about the axis of rotation and the wake rotation
velocity will lie in a plane normal to the skewed wake axis.
To determine the wake rotation velocity the rate of change of angular momentum
about the skewed wake axis will be equated to the moment about the axis produced
by blade forces.
If the wake rotation velocity is described, as before, in terms of the angular
velocity of the rotor then

v- ¼ Ùr-a9h(ł) (3:125)
where the triple prime denotes an axis system rotating about the wake axis and h(Ł)
is a function which determines the intensity of the root vortex’s influence. In the
non-yawed case the root vortex induces a velocity at the rotor which is half of that it
induces in the far wake at the same radial distance and the same would apply to a
disc normal to the skewed axis with a centre located at the same position as the