Page 332 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

T1: IML
QC: IML/FFX
P2: IML/FFX
P1: IML/FFX
June 22, 2007
17:40
AT029-07
AT029-Manual-v7.cls
AT029-Manual
312 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
is normally used at superatmospheric pressures where nor-
1000
mal boiling point (T b ) is known and boiling point at higher
100 pressures (T) is required. When calculation of vapor pressure
(P vap ) at a given temperature (T) is required, Eq. (3.29) can
Vapor Pressure, bar 1 Data log 10 P vap = 3000.538Q − 6.761560 vap
be rearranged in the following form:
10
43Q − 0.987672
for Q > 0.0022 (P
0.1
Lee-Kesler
Ambrose-Walton 2663.129Q − 5.994296 < 2 mm Hg)
0.01 Antoine log 10 P vap = 95.76Q − 0.972546
0.001
for 0.0013 ≤ Q ≤ 0.0022(2 mm Hg ≤ P vap ≤ 760 mm Hg)
0 50 100 150 200 250 300 350 400
Temperature, C vap 2770.085Q − 6.412631
log 10 P =
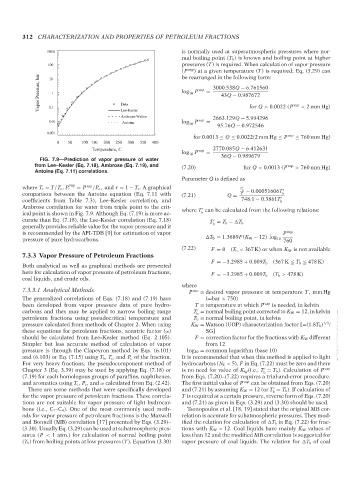
FIG. 7.9—Prediction of vapor pressure of water 36Q − 0.989679
from Lee–Kesler (Eq. 7.18), Ambrose (Eq. 7.19), and (7.20) for Q < 0.0013 (P vap > 760 mm Hg)
Antoine (Eq. 7.11) correlations.
Parameter Q is defined as
vap vap
where T r = T/T c , P r = P /P c , and τ = 1 − T r . A graphical T b − 0.00051606T
comparison between the Antoine equation (Eq. 7.11 with (7.21) Q = T b
coefficients from Table 7.3), Lee–Kesler correlation, and 748.1 − 0.3861T b
Ambrose correlation for water from triple point to the crit- where T can be calculated from the following relations:

ical point is shown in Fig. 7.9. Although Eq. (7.19) is more ac- b
curate than Eq. (7.18), the Lee–Kesler correlation (Eq. 7.18)
T = T b − T b
b
generally provides reliable value for the vapor pressure and it
is recommended by the API-TDB [9] for estimation of vapor P vap
pressure of pure hydrocarbons. T b = 1.3889F(K W − 12) log 10 760
(7.22) F = 0(T b < 367 K) or when K W is not available
7.3.3 Vapor Pressure of Petroleum Fractions
(367 K ≤ T b ≤ 478 K)
F =−3.2985 + 0.009T b
Both analytical as well as graphical methods are presented
here for calculation of vapor pressure of petroleum fractions,
F =−3.2985 + 0.009T b (T b > 478 K)
coal liquids, and crude oils.
where
7.3.3.1 Analytical Methods P vap = desired vapor pressure at temperature T,mm Hg
The generalized correlations of Eqs. (7.18) and (7.19) have (=bar × 750)
been developed from vapor pressure data of pure hydro- T = temperature at which P vap is needed, in kelvin
carbons and they may be applied to narrow boiling range T = normal boiling point corrected to K W = 12, in kelvin

b
petroleum fractions using pseudocritical temperature and T b = normal boiling point, in kelvin
pressure calculated from methods of Chapter 2. When using K W = Watson (UOP) characterization factor [=(1.8T b ) 1/3 /
these equations for petroleum fractions, acentric factor (ω) SG]
should be calculated from Lee–Kesler method (Eq. 2.105). F = correction factor for the fractions with K W different --`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
Simpler but less accurate method of calculation of vapor from 12
pressure is through the Clapeyron method by Eqs. (6.101) log 10 = common logarithm (base 10)
and (6.103) or Eq. (7.15) using T b , T c , and P c of the fraction. It is recommended that when this method is applied to light
For very heavy fractions, the pseudocomponent method of hydrocarbons (N C < 5), F in Eq. (7.22) must be zero and there
Chapter 3 (Eq. 3.39) may be used by applying Eq. (7.18) or is no need for value of K (i.e., T = T b ). Calculation of P vap

b
W
(7.19) for each homologous groups of paraffins, naphthenes, from Eqs. (7.20)–(7.22) requires a trial-and-error procedure.
and aromatics using T c , P c , and ω calculated from Eq. (2.42). The first initial value of P vap can be obtained from Eqs. (7.20)
There are some methods that were specifically developed and (7.21) by assuming K W = 12 (or T = T b ). If calculation of

b
for the vapor pressure of petroleum fractions. These correla- T is required at a certain pressure, reverse form of Eqs. (7.20)
tions are not suitable for vapor pressure of light hydrocar- and (7.21) as given in Eqs. (3.29) and (3.30) should be used.
bons (i.e., C 1 –C 4 ). One of the most commonly used meth- Tsonopoulos et al. [18, 19] stated that the original MB cor-
ods for vapor pressure of petroleum fractions is the Maxwell relation is accurate for subatmospheric pressures. They mod-
and Bonnell (MB) correlation [17] presented by Eqs. (3.29)– ified the relation for calculation of T b in Eq. (7.22) for frac-
(3.30). Usually Eq. (3.29) can be used at subatmospheric pres- tions with K W < 12. Coal liquids have mainly K W values of
sures (P < 1 atm.) for calculation of normal boiling point less than 12 and the modified MB correlation is suggested for
(T b ) from boiling points at low pressures (T). Equation (3.30) vapor pressure of coal liquids. The relation for T b of coal

Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT