Page 376 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

P1: JDW
AT029-Manual
AT029-Manual-v7.cls
AT029-08
356 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
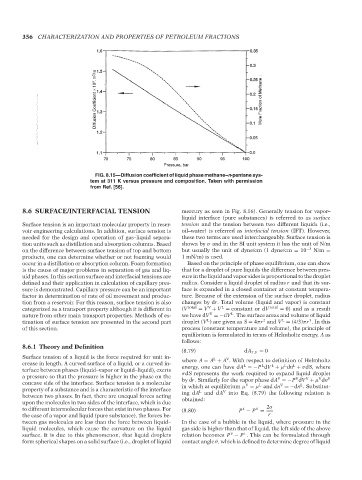
Diffusion Coefficient × 10 5 , m 2 / s June 22, 2007 14:25 Mole Fraction of Methane

--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---

Pressure, bar
FIG. 8.15—Diffusion coefficient of liquid phase methane–n-pentane sys-
tem at 311 K versus pressure and composition. Taken with permission
from Ref. [56].

8.6 SURFACE/INTERFACIAL TENSION mercury as seen in Fig. 8.16). Generally tension for vapor–
liquid interface (pure substances) is referred to as surface
Surface tension is an important molecular property in reser- tension and the tension between two different liquids (i.e.,
voir engineering calculations. In addition, surface tension is oil–water) is referred as interfacial tension (IFT). However,
needed for the design and operation of gas–liquid separa- these two terms are used interchangeably. Surface tension is
tion units such as distillation and absorption columns. Based shown by σ and in the SI unit system it has the unit of N/m
on the difference between surface tension of top and bottom but usually the unit of dyne/cm (1 dyne/cm = 10 −3 N/m =
products, one can determine whether or not foaming would 1 mN/m) is used.
occur in a distillation or absorption column. Foam formation Based on the principle of phase equilibrium, one can show
is the cause of major problems in separation of gas and liq- that for a droplet of pure liquids the difference between pres-
uid phases. In this section surface and interfacial tensions are sure in the liquid and vapor sides is proportional to the droplet
defined and their application in calculation of capillary pres- radius. Consider a liquid droplet of radius r and that its sur-
sure is demonstrated. Capillary pressure can be an important face is expanded in a closed container at constant tempera-
factor in determination of rate of oil movement and produc- ture. Because of the extension of the surface droplet, radius
tion from a reservoir. For this reason, surface tension is also changes by dr. Total volume (liquid and vapor) is constant
L
V
categorized as a transport property although it is different in (V total = V + V = constant or dV total = 0) and as a result
L
V
nature from other main transport properties. Methods of es- we have dV =−dV . The surface areas and volume of liquid
3
L
L
2
timation of surface tension are presented in the second part droplet (V ) are given as S = 4πr and V = (4/3)πr . In this
of this section. process (constant temperature and volume), the principle of
equilibrium is formulated in terms of Helmholtz energy, A as
follows:
8.6.1 Theory and Definition
(8.79) dA T,V = 0
Surface tension of a liquid is the force required for unit in- where A = A + A . With respect to definition of Helmholtz
L
V
crease in length. A curved surface of a liquid, or a curved in- L L L L L
terface between phases (liquid–vapor or liquid–liquid), exerts energy, one can have dA =−P dV + μ dn + σdS, where
a pressure so that the pressure is higher in the phase on the σdS represents the work required to expand liquid droplet
V
V
V
V
V
concave side of the interface. Surface tension is a molecular by dr. Similarly for the vapor phase dA =−P dV + μ dn
L
L
V
V
property of a substance and is a characteristic of the interface in which at equilibrium μ = μ and dn =−dn . Substitut-
L
V
between two phases. In fact, there are unequal forces acting ing dA and dA into Eq. (8.79) the following relation is
upon the molecules in two sides of the interface, which is due obtained:
to different intermolecular forces that exist in two phases. For (8.80) P − P = 2σ
V
L
the case of a vapor and liquid (pure substance), the forces be- r
tween gas molecules are less than the force between liquid– In the case of a bubble in the liquid, where pressure in the
liquid molecules, which cause the curvature on the liquid gas side is higher than that of liquid, the left side of the above
L
V
surface. It is due to this phenomenon, that liquid droplets relation becomes P − P . This can be formulated through
form spherical shapes on a solid surface (i.e., droplet of liquid contact angle θ, which is defined to determine degree of liquid
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT