Page 378 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

P1: JDW
AT029-Manual-v7.cls
AT029-Manual
AT029-08
358 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
TABLE 8.13—Values of surface tension of some
hydrocarbons at 25 C [45]. June 22, 2007 14:25
◦
Naphthenic Acid
Compound σ at 25 C, dyne/cm θ=106 o
◦
n-Pentane 15.47
n-Decane 23.39
n-Pentadecane 26.71
n-Eicosane 28.56 Water
n-Hexatriacontane 30.44
Cyclopentane 21.78
Cyclohexane 24.64
Benzene 28.21
Decylbenzene 30.52 Calcite
Pentadecylbenzene 31.97
Water (at 15 C) 74.83
◦
Water (at 25 C) 72.82
◦
Iso-Octane
for pure hydrocarbons and water are given in Table 8.13. Sur- θ=30 o
face tension increases from paraffins to naphthenes and to
aromatics for a same carbon number. Water has significantly Water
higher surface tension than hydrocarbons. Surface tension
of mercury is quite high and at 20 C it is 476 mN/m. Liquid Calcite
◦
metals have even higher surface tensions [18].
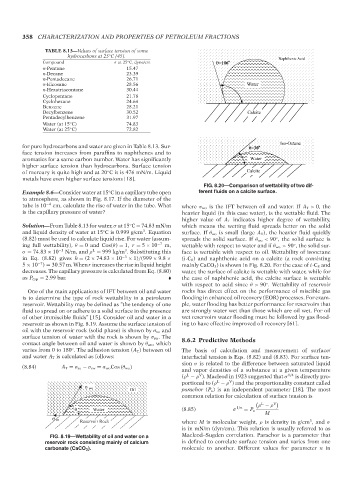
FIG. 8.20—Comparison of wettability of two dif-
Example 8.6—Consider water at 15 C in a capillary tube open ferent fluids on a calcite surface.
◦
to atmosphere, as shown in Fig. 8.17. If the diameter of the
tube is 10 −4 cm, calculate the rise of water in the tube. What where σ wo is the IFT between oil and water. If A T > 0, the
is the capillary pressure of water? heavier liquid (in this case water), is the wettable fluid. The
higher value of A T indicates higher degree of wettability,
Solution—From Table 8.13 for water, σ at 15 C = 74.83 mN/m which means the wetting fluid spreads better on the solid
◦
3
and liquid density of water at 15 C is 0.999 g/cm . Equation surface. If θ wo is small (large A T ), the heavier fluid quickly
◦
(8.82) must be used to calculate liquid rise. For water (assum- spreads the solid surface. If θ wo < 90 , the solid surface is
◦
ing full wettability), θ = 0 and Cos(θ) = 1, r = 5 × 10 −7 m, wettable with respect to water and if θ wo > 90 , the solid sur-
◦
3
L
σ = 74.83 × 10 −3 N/m, and ρ = 999 kg/m . Substituting this face is wettable with respect to oil. Wettability of isooctane
in Eq. (8.82) gives h = (2 × 74.83 × 10 −3 × 1)/(999 × 9.8 × (i-C 8 ) and naphthenic acid on a calcite (a rock consisting
−7
5 × 10 ) = 30.57 m. When r increases the rise in liquid height mainly CaCO 3 ) is shown in Fig. 8.20. For the case of i-C 8 and
decreases. The capillary pressure is calculated from Eq. (8.80) water, the surface of calcite is wettable with water, while for
as P cap = 2.99 bar. the case of naphthenic acid, the calcite surface is wettable
with respect to acid since θ> 90 . Wettability of reservoir
◦
One of the main applications of IFT between oil and water rocks has direct effect on the performance of miscible gas
is to determine the type of rock wettability in a petroleum flooding in enhanced oil recovery (EOR) processes. For exam-
reservoir. Wettability may be defined as “the tendency of one ple, water flooding has better performance for reservoirs that
fluid to spread on or adhere to a solid surface in the presence are strongly water wet than those which are oil wet. For oil
of other immiscible fluids” [15]. Consider oil and water in a wet reservoirs water flooding must be followed by gas flood-
reservoir as shown in Fig. 8.19. Assume the surface tension of ing to have effective improved oil recovery [61].
oil with the reservoir rock (solid phase) is shown by σ so and
surface tension of water with the rock is shown by σ sw . The 8.6.2 Predictive Methods
contact angle between oil and water is shown by θ wo , which
varies from 0 to 180 . The adhesion tension (A T ) between oil The basis of calculation and measurement of surface/
◦
and water A T is calculated as follows: interfacial tension is Eqs. (8.82) and (8.83). For surface ten-
sion σ is related to the difference between saturated liquid
(8.84) A T = σ so − σ sw = σ wo Cos (θ wo)
and vapor densities of a substance at a given temperature
L
V
(ρ − ρ ). Macleod in 1923 suggested that σ 1/4 is directly pro-
L
V
portional to (ρ − ρ ) and the proportionality constant called
σ wo
Oil parachor (P a ) is an independent parameter [18]. The most
common relation for calculation of surface tension is
o
θ=30
L V
ρ − ρ
1/n
θ Water (8.85) σ = P a
M
σ so 3
Reservoir Rock where M is molecular weight, ρ is density in g/cm , and σ
is in mN/m (dyn/cm). This relation is usually referred to as
FIG. 8.19—Wettability of oil and water on a Macleod–Sugden correlation. Parachor is a parameter that
reservoir rock consisting mainly of calcium is defined to correlate surface tension and varies from one
carbonate (CaCO 3 ). molecule to another. Different values for parameter n in
--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT