Page 258 - Petroleum Production Engineering, A Computer-Assisted Approach

Guo, Boyun / Computer Assited Petroleum Production Engg 0750682701_chap17 Final Proof page 257 3.1.2007 9:19pm Compositor Name: SJoearun

HYDRAULIC FRACTURING 17/257
In the situations in which the fracture dimension is much The previous analyses reveal that low-permeability res-
less than the drainage area of the well, the long-term ervoirs, leading to high-conductivity fractures, would
productivity of the fractured well can be estimated assum- benefit greatly from fracture length, whereas high-perme-
ing pseudo-radial flow in the reservoir. Then the inflow ability reservoirs, naturally leading to low-conductivity
equation can be written as fractures, require good fracture permeability and width.
Valko et al. (1997) converted the data in Fig. 17.7 into
kh p e p wf
q ¼ , (17:11) the following correlation:
141:2Bm ln r e þ S f 2
r w x f 1:65 0:328u þ 0:116u
s f þ ln ¼ (17:15)
2
where S f is the equivalent skin factor. The fold of increase r w 1 þ 0:180u þ 0:064u þ 0:05u 3
can be expressed as where
J ln r e u ¼ ln (F CD ) (17:16)
¼ r w , (17:12)
J o ln r e þ S f
r w
where Example Problem 17.2 A gas reservoir has a permeability
J ¼ productivity of fractured well, stb/day-psi of 1 md. A vertical well of 0.328-ft radius draws the
J o ¼ productivity of nonfractured well, reservoir from the center of an area of 160 acres. If the
stb/day-psi. well is hydraulically fractured to create a 2,000-ft long,
0.12-in. wide fracture of 200,000 md permeability around
The effective skin factor S f can be determined based on the center of the drainage area, what would be the fold of
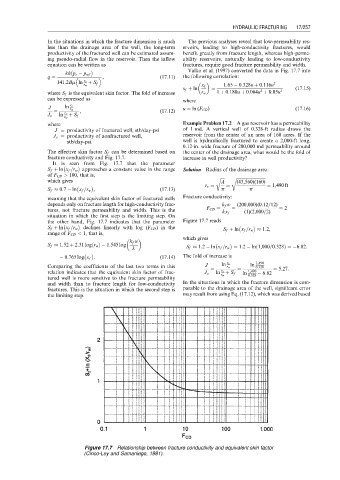
fracture conductivity and Fig. 17.7. increase in well productivity?
It is seen from Fig. 17.7 that the parameter

S f þ ln x f =r w approaches a constant value in the range Solution Radius of the drainage area:
of F CD > 100, that is, r ffiffiffiffi r ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
which gives A (43,560)(160)
r e ¼ ¼ ¼ 1,490 ft
S f 0:7 ln x f =r w , (17:13) p p
meaning that the equivalent skin factor of fractured wells Fracture conductivity:
depends only on fracture length for high-conductivity frac- k f w (200,000)(0:12=12)
tures, not fracture permeability and width. This is the F CD ¼ ¼ (1)(2,000=2) ¼ 2
kx f
situation in which the first step is the limiting step. On
the other hand, Fig. 17.7 indicates that the parameter Figure 17.7 reads

declines linearly with log (F CD ) in the
S f þ ln x f =r w S f þ ln x f =r w 1:2,
range of F CD < 1, that is,
which gives
k f w
ðÞ
S f 1:52 þ 2:31 log r w 1:545 log S f 1:2 ln x f =r w ¼ 1:2 ln 1,000=0:328ð Þ ¼ 6:82:
k

0:765 log x f : (17:14) The fold of increase is
Comparing the coefficients of the last two terms in this J ¼ ln r w r e ¼ ln 1,490 ¼ 5:27:
0:328
relation indicates that the equivalent skin factor of frac- ln r e ln 1,490 6:82
J o
r w þ S f 0:328
tured well is more sensitive to the fracture permeability
and width than to fracture length for low-conductivity In the situations in which the fracture dimension is com-
fractures. This is the situation in which the second step is parable to the drainage area of the well, significant error
the limiting step. may result from using Eq. (17.12), which was derived based

Figure 17.7 Relationship between fracture conductivity and equivalent skin factor
(Cinco-Ley and Samaniego, 1981).