Page 48 - Petroleum Production Engineering, A Computer-Assisted Approach

Guo, Boyun / Computer Assited Petroleum Production Engg 0750682701_chap03 Final Proof page 38 3.1.2007 8:30pm Compositor Name: SJoearun

3/38 PETROLEUM PRODUCTION ENGINEERING FUNDAMENTALS
3,500

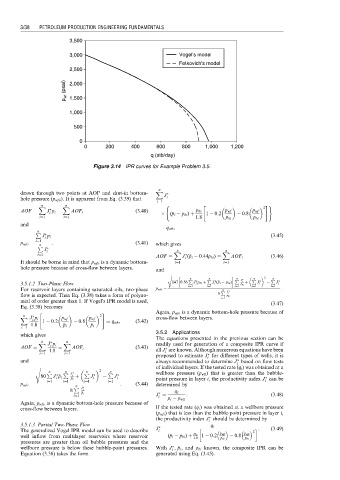
3,000 Vogel's model
Fetkovich's model
2,500
p wf (psai) 2,000

1,500

1,000

500

0
0 200 400 600 800 1,000 1,200
q (stb/day)
Figure 3.14 IPR curves for Example Problem 3.5.

X
n
drawn through two points at AOF and shut-in bottom- J
hole pressure (p wfo ). It is apparent from Eq. (3.39) that i
i¼1
X X ( " 2 #)
n
n

AOF ¼ J p i ¼ AOF i (3:40) ( p i p bi ) þ p bi 1 0:2 p wf 0:8 p wf
p
p
i
i¼1 i¼1 1:8 p bi p bi
and
¼ q wh ,
P
n
p
J p i (3:45)
i
p wfo ¼ i¼1 : (3:41) which gives
P
n
J i X X
n
n
i¼1
AOF ¼ J ( p i 0:44p bi ) ¼ AOF i (3:46)
p
i
It should be borne in mind that p wfo is a dynamic bottom- i¼1 i¼1
hole pressure because of cross-flow between layers. and
s ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi

P P P J P n 2 P n
n
n
n

p
3.5.1.2 Two-Phase Flow 147 0:56 J i p bi þ J i ( p i p bi ) p bi i þ J i J i
For reservoir layers containing saturated oils, two-phase p wfo ¼ i¼1 i¼1 P J i¼1 i¼1 i¼1 :
n
flow is expected. Then Eq. (3.38) takes a form of polyno- 8 i¼1 p bi i
mial of order greater than 1. If Vogel’s IPR model is used, (3:47)
Eq. (3.38) becomes
" # Again, p wfo is a dynamic bottom-hole pressure because of
n
X p 2 cross-flow between layers.
J p i 1 0:2 p wf 0:8 p wf ¼ q wh , (3:42)
i
1:8
i¼1 p p i p p i
3.5.2 Applications
which gives
The equations presented in the previous section can be
n
X p X readily used for generation of a composite IPR curve if
n
i
AOF ¼ J p i ¼ AOF i (3:43)
1:8 all J are known. Although numerous equations have been
i¼1 i¼1 i
proposed to estimate J for different types of wells, it is
i

and always recommended to determine J based on flow tests
i
s ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi of individual layers. If the tested rate (q i ) was obtained at a

n
n
n
P P J P 2 P wellbore pressure (p wfi ) that is greater than the bubble-
n

p
80 J p i i þ J i J i point pressure in layer i, the productivity index J can be

i
i¼1 i¼1 p p i i¼1 i¼1 i
p wfo ¼ n : (3:44) determined by
P J
8 i
p p i q i
i¼1 J ¼ : (3:48)
i
p p i p wfi
Again, p wfo is a dynamic bottom-hole pressure because of
cross-flow between layers. If the tested rate (q i ) was obtained at a wellbore pressure
(p wfi ) that is less than the bubble-point pressure in layer i,

the productivity index J should be determined by
i
3.5.1.3 Partial Two-Phase Flow q i
The generalized Vogel IPR model can be used to describe J ¼ 2 : (3:49)
i
p
well inflow from multilayer reservoirs where reservoir ( p i p bi ) þ p bi 1 0:2 p wfi 0:8 p wfi
1:8
p bi
p bi
pressures are greater than oil bubble pressures and the

wellbore pressure is below these bubble-point pressures. With J , p i , and p bi known, the composite IPR can be
p
i
Equation (3.38) takes the form generated using Eq. (3.45).