Page 343 - Acquisition and Processing of Marine Seismic Data

334 6. DECONVOLUTION

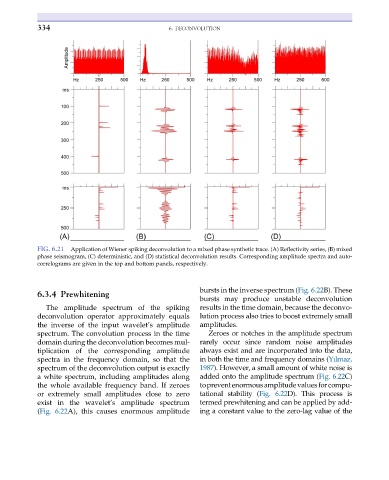
FIG. 6.21 Application of Wiener spiking deconvolution to a mixed phase synthetic trace. (A) Reflectivity series, (B) mixed
phase seismogram, (C) deterministic, and (D) statistical deconvolution results. Corresponding amplitude spectra and auto-
correlograms are given in the top and bottom panels, respectively.

bursts in the inverse spectrum (Fig. 6.22B). These
6.3.4 Prewhitening
bursts may produce unstable deconvolution
The amplitude spectrum of the spiking results in the time domain, because the deconvo-
deconvolution operator approximately equals lution process also tries to boost extremely small
the inverse of the input wavelet’s amplitude amplitudes.
spectrum. The convolution process in the time Zeroes or notches in the amplitude spectrum
domain during the deconvolution becomes mul- rarely occur since random noise amplitudes
tiplication of the corresponding amplitude always exist and are incorporated into the data,
spectra in the frequency domain, so that the in both the time and frequency domains (Yılmaz,
spectrum of the deconvolution output is exactly 1987). However, a small amount of white noise is
a white spectrum, including amplitudes along added onto the amplitude spectrum (Fig. 6.22C)
the whole available frequency band. If zeroes topreventenormousamplitudevaluesforcompu-
or extremely small amplitudes close to zero tational stability (Fig. 6.22D). This process is
exist in the wavelet’s amplitude spectrum termed prewhitening and can be applied by add-
(Fig. 6.22A), this causes enormous amplitude ing a constant value to the zero-lag value of the