Page 489 - Acquisition and Processing of Marine Seismic Data

480 10. NORMAL MOVEOUT CORRECTION AND STACKING

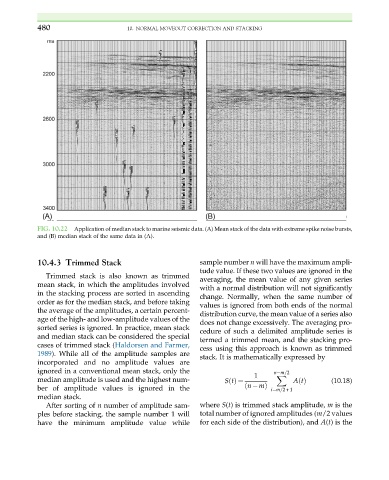
FIG. 10.22 Application of median stack to marine seismic data. (A) Mean stack of the data with extreme spike noise bursts,
and (B) median stack of the same data in (A).

10.4.3 Trimmed Stack sample number n will have the maximum ampli-
tude value. If these two values are ignored in the
Trimmed stack is also known as trimmed
averaging, the mean value of any given series
mean stack, in which the amplitudes involved
with a normal distribution will not significantly
in the stacking process are sorted in ascending
change. Normally, when the same number of
order as for the median stack, and before taking
values is ignored from both ends of the normal
the average of the amplitudes, a certain percent-
distribution curve, the mean value of a series also
age of the high- and low-amplitude values of the
does not change excessively. The averaging pro-
sorted series is ignored. In practice, mean stack
cedure of such a delimited amplitude series is
and median stack can be considered the special
termed a trimmed mean, and the stacking pro-
cases of trimmed stack (Haldorsen and Farmer,
cess using this approach is known as trimmed
1989). While all of the amplitude samples are stack. It is mathematically expressed by
incorporated and no amplitude values are
ignored in a conventional mean stack, only the n m=2
1 X
median amplitude is used and the highest num- StðÞ ¼ AtðÞ (10.18)
ber of amplitude values is ignored in the ð n mÞ i¼m=2+1
median stack.
After sorting of n number of amplitude sam- where S(t) is trimmed stack amplitude, m is the
ples before stacking, the sample number 1 will total number of ignored amplitudes (m/2 values
have the minimum amplitude value while for each side of the distribution), and A(t) is the