Page 312 - Advanced Organic Chemistry Part A - Structure and Mechanisms, 5th ed (2007) - Carey _ Sundberg

important. Whatever the nature of the substituent effects, the Hammond postulate 293
recognizes that structural discussion of transition states in terms of reactants, interme-
diates, or products is valid only when their structures and energies are similar. SECTION 3.3
General Relationships
between Thermodynamic
3.3.2.3. The Marcus Equation. The Marcus equation provides a means for numerical Stability and Reaction
o
‡
evaluation of the relationship between G and G . The Marcus equation proposes Rates
that for a single-step reaction process there is a relationship involving the net exo- or
endothermicity of the reaction and an energy associated with the activation process
59
called the intrinsic barrier. The Marcus equation proposes that for a series of related
‡
o
reactions, there is a predictable relationship between G and G , the free energy of
reaction. The energies of the reactants, transition state, and products can be described
by intersecting parabolic potential energy functions. The relationship can be expressed
by the following equation:
‡
o
G = G 1+ G /4G 2 (3.33)
˜
˜
‡
o
˜
where G is the intrinsic barrier of the reaction and G and G are free energy and
energy of activation for the reaction under consideration.
The Marcus equation (3.33), like the Bell-Evans-Polyani relationship, indicates
that for a related series of reactions, the activation energy (and therefore the rate) is
related to the net free-energy change. It is based on assumption of a parabolic shape of
the potential energy curve and breaks down at certain limits. The range of the equation
can be extended by other formulations of the shape of the potential energy functions. 60
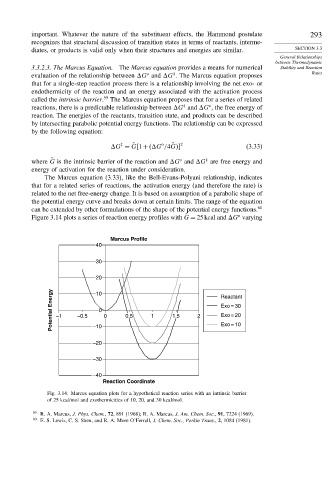
o
Figure 3.14 plots a series of reaction energy profiles with G = 25kcal and G varying
˜
Marcus Profile
40

30

20
Potential Energy –1 –0.5 –10 0 0.5 1 1.5 2 Reactant
10
Exo = 30
0
Exo = 20
Exo = 10

–20

–30

–40
Reaction Coordinate
Fig. 3.14. Marcus equation plots for a hypothetical reaction series with an intrinsic barrier
of 25 kcal/mol and exothermicities of 10, 20, and 30 kcal/mol.
59 R. A. Marcus, J. Phys. Chem., 72, 891 (1968); R. A. Marcus, J. Am. Chem. Soc., 91, 7224 (1969).
60
E. S. Lewis, C. S. Shen, and R. A. More O’Ferrall, J. Chem. Soc., Perkin Trans., 2, 1084 (1981).