Page 428 - Analog and Digital Filter Design

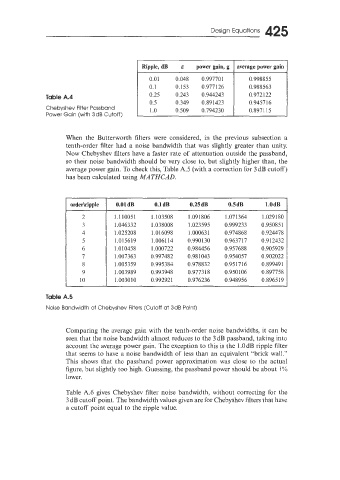
Design Equations 425

0.153 0.977126
Table A.4 0.25 0.243 0.944243
0.349 0.891423
Chebyshev Filter Passband
Power Gain (with 3dB Cutoff)

When the Butterworth filters were considered, in the previous subsection a
tenth-order filter had a noise bandwidth that was slightly greater than unity.
Now Chebyshev filters have a faster rate of attenuation outside the passband,
so their noise bandwidth should be very close to, but slightly higher than, the
average power gain. To check this, Table A.5 (with a correction for 3 dB cutoff)
has been calculated using MATHCAD.

orderhipple 0.01 dB 0.1 dB 0.25 dB 0.5 dB l.OdB
2 1.110051 1.103508 1.09 1806 1.07 I 364 1.029180
3 1.046332 1.038008 1.023595 0.999233 0.950851
4 1.025208 1.016098 1.00063 1 0.974868 0.924478
5 1 .O 15619 1.0061 14 0.990130 0.963717 0.912432
6 1.010458 1.000722 0.984456 0.957688 0.905929
7 1.007363 0.997482 0.981043 0.9 540 5 7 0.902022
8 1.005359 0.995384 0.978832 0.95 17 16 0.89949 1
9 1.003989 0.993948 0.9773 18 0.950106 0.897758
10 1.003010 0.99292 1 0.976236 0.948956 0.896519

Table A.5
Noise Bandwidth of Chebyshev Filters (Cutoff at 3dB Point)

Comparing the average gain with the tenth-order noise bandwidths, it can be
seen that the noise bandwidth almost reduces to the 3 dB passband, taking into
account the average power gain. The exception to this is the 1.0dB ripple filter
that seems to have a noise bandwidth of less than an equivalent "brick wal!."
This shows that the passband power approximation was close to the actual
figure, but slightly too high. Guessing, the passband power should be about 1%
lower.

Table A.6 gives Chebyshev filter noise bandwidth, without correcting for the
3 dB cutoff point. The bandwidth values given are for Chebyshev filters that have
a cutoff point equal to the ripple value.