Page 322 - Applied Numerical Methods Using MATLAB

PROBLEMS 311
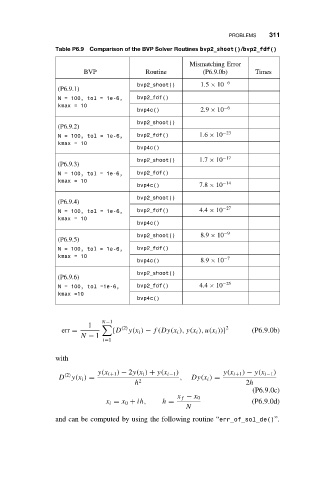
Table P6.9 Comparison of the BVP Solver Routines bvp2 shoot()/bvp2 fdf()

Mismatching Error
BVP Routine (P6.9.0b) Times
bvp2 shoot() 1.5 × 10 −6
(P6.9.1)
N = 100, tol = 1e-6, bvp2 fdf()
kmax = 10 −6
bvp4c() 2.9 × 10
bvp2 shoot()
(P6.9.2)
N = 100, tol = 1e-6, bvp2 fdf() 1.6 × 10 −23
kmax = 10
bvp4c()
bvp2 shoot() 1.7 × 10 −17
(P6.9.3)
N = 100, tol = 1e-6, bvp2 fdf()
kmax = 10
bvp4c() 7.8 × 10 −14
bvp2 shoot()
(P6.9.4)
N = 100, tol = 1e-6, bvp2 fdf() 4.4 × 10 −27
kmax = 10
bvp4c()
bvp2 shoot() 8.9 × 10 −9
(P6.9.5)
N = 100, tol = 1e-6, bvp2 fdf()
kmax = 10 −7
bvp4c() 8.9 × 10
bvp2 shoot()
(P6.9.6)
N = 100, tol =1e-6, bvp2 fdf() 4.4 × 10 −25
kmax =10
bvp4c()

N−1
1 (2) 2
err = {D y(x i ) − f(Dy(x i ), y(x i ), u(x i ))} (P6.9.0b)
N − 1
i=1
with
y(x i+1 ) − 2y(x i ) + y(x i−1 ) y(x i+1 ) − y(x i−1 )
(2)
D y(x i ) = , Dy(x i ) =
h 2 2h
(P6.9.0c)
x f − x 0
x i = x 0 + ih, h = (P6.9.0d)
N
and can be computed by using the following routine “err_of_sol_de()”.