Page 244 - Applied Statistics And Probability For Engineers

c06.qxd 5/14/02 9:55 M Page 205 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark Files:

6-4 FREQUENCY DISTRIBUTIOINS AND HISTOGRAMS 205

20

10

Frequency 5 Frequency 10

0
0
100 150 200 250 80 100 120 140 160 180 200 220 240
Strength Strength
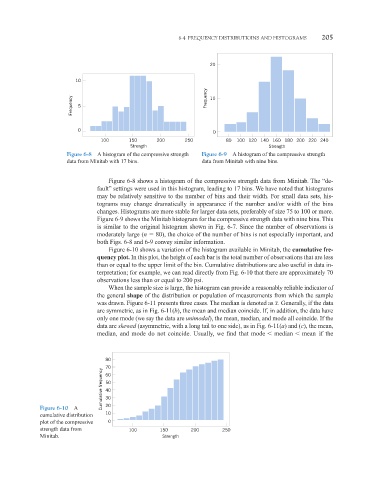
Figure 6-8 A histogram of the compressive strength Figure 6-9 A histogram of the compressive strength
data from Minitab with 17 bins. data from Minitab with nine bins.

Figure 6-8 shows a histogram of the compressive strength data from Minitab. The “de-
fault” settings were used in this histogram, leading to 17 bins. We have noted that histograms
may be relatively sensitive to the number of bins and their width. For small data sets, his-
tograms may change dramatically in appearance if the number and/or width of the bins
changes. Histograms are more stable for larger data sets, preferably of size 75 to 100 or more.
Figure 6-9 shows the Minitab histogram for the compressive strength data with nine bins. This
is similar to the original histogram shown in Fig. 6-7. Since the number of observations is
moderately large (n 80), the choice of the number of bins is not especially important, and
both Figs. 6-8 and 6-9 convey similar information.
Figure 6-10 shows a variation of the histogram available in Minitab, the cumulative fre-
quency plot. In this plot, the height of each bar is the total number of observations that are less
than or equal to the upper limit of the bin. Cumulative distributions are also useful in data in-
terpretation; for example, we can read directly from Fig. 6-10 that there are approximately 70
observations less than or equal to 200 psi.
When the sample size is large, the histogram can provide a reasonably reliable indicator of
the general shape of the distribution or population of measurements from which the sample
~
x
was drawn. Figure 6-11 presents three cases. The median is denoted as . Generally, if the data
are symmetric, as in Fig. 6-11(b), the mean and median coincide. If, in addition, the data have
only one mode (we say the data are unimodal), the mean, median, and mode all coincide. If the
data are skewed (asymmetric, with a long tail to one side), as in Fig. 6-11(a) and (c), the mean,
median, and mode do not coincide. Usually, we find that mode median mean if the

80
70
Cumulative frequency 50
60

40
30
Figure 6-10 A 20
cumulative distribution 10
plot of the compressive 0
strength data from 100 150 200 250
Minitab. Strength